Предмет: Алгебра,
автор: vityamath
Найдите область значений функции, не пользуясь производной:
Приложения:
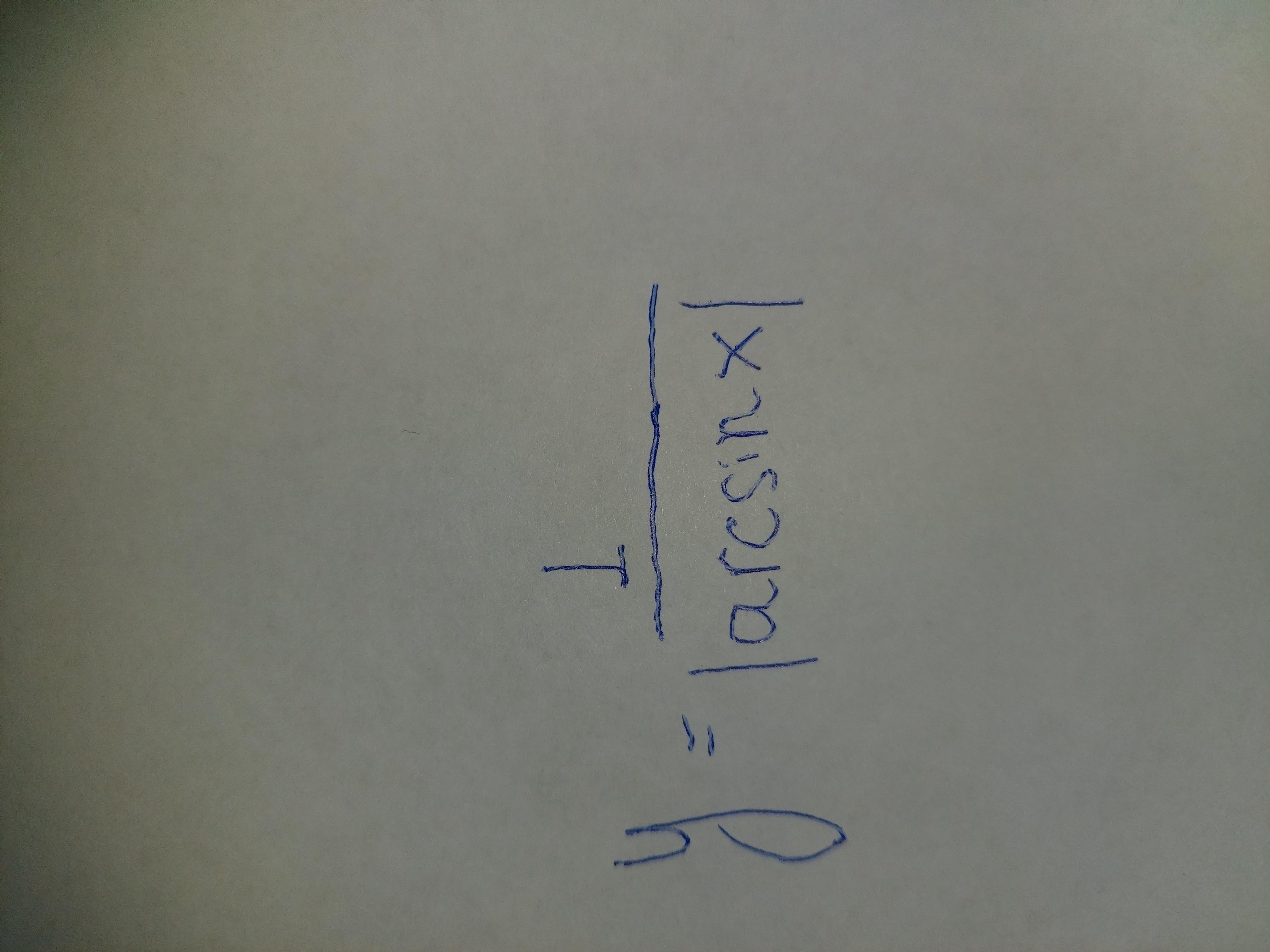
terikovramazan:
[2/pi; +беск) ?
Ответы
Автор ответа:
3
Для выполнения задания нужно знать область значений функции arcsin(x) [-π/2;π/2]
Когда х стремится к нулю ( х ≠ 0, по ОДЗ) то значение функции стремится к ∞.
Похожие вопросы
Предмет: Қазақ тiлi,
автор: ЕвангелинаМорозова
Предмет: Қазақ тiлi,
автор: пери8
Предмет: Русский язык,
автор: Nara30
Предмет: Русский язык,
автор: ulugyunayy28
Предмет: Литература,
автор: olya9056