Предмет: Математика,
автор: Parter78
Найдите общее решение дифференциального уравнения второго порядка, которое допускает понижение порядка.
Приложения:
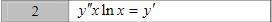
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Hariton2015
Предмет: Русский язык,
автор: kadykov2003
Предмет: Физика,
автор: Alina23089