Предмет: Алгебра,
автор: daslight19
помогите пжалста хоть с чем то из этого СРОЧНО!!!
Приложения:
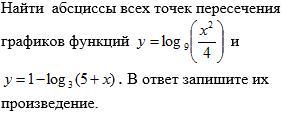
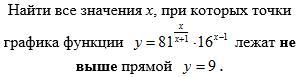
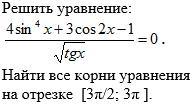
Ответы
Автор ответа:
2
Ответ:
Объяснение:
по Виета
не удовлетворяет
найдем произведение корней
1 · (-2) · (-3) = 6
О т в е т : 6
Похожие вопросы
Предмет: Русский язык,
автор: vova237
Предмет: Русский язык,
автор: anton00342
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: RomtsovaJulia003