Предмет: Геометрия,
автор: Chikrygina
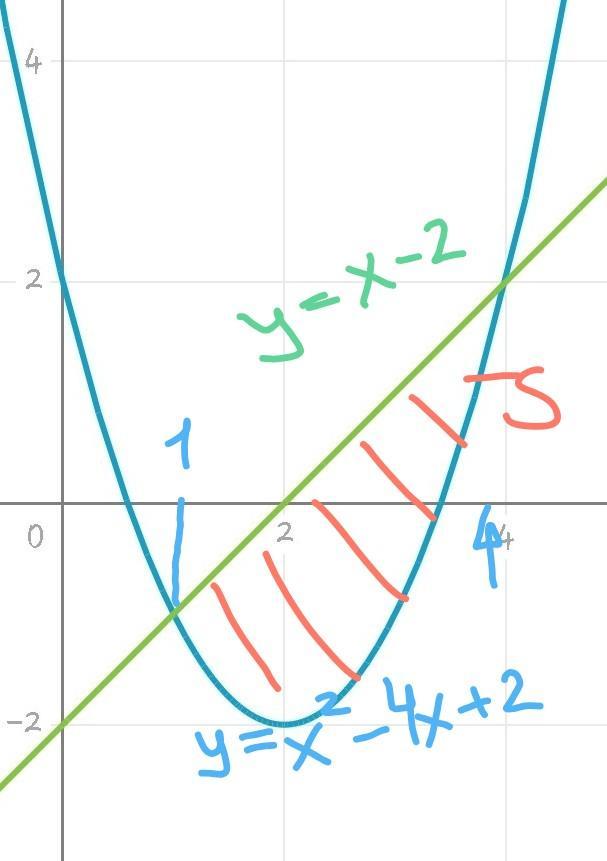
Вычислите площадь фигуры, ограниченной прямой y=x-2 и параболой
y=x²-4x+2
Ответы
Автор ответа:
1
Ответ:
- точки пересечения (и пределы интегрирования)
рисунок
Приложения:
Автор ответа:
2
Ответ 4,5
Решение задания прилагаю
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: xaza502gast123p
Предмет: Русский язык,
автор: shsjs1
Предмет: Окружающий мир,
автор: ева4160
Предмет: Английский язык,
автор: Angelica161
Предмет: Українська мова,
автор: ДанилСергеев1234568