Предмет: Математика,
автор: sobakazabiyaka
Найти угол между градиентами функций u и v в точке М0
Приложения:
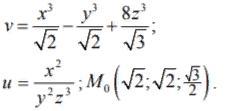
Ответы
Автор ответа:
3
ОТВЕТ: , или
.
Объяснение: Найдем частные производные 1-го порядка функции :
Градиент функции :
Аналогичным образом находим градиент функции в точке
:
По определению скалярного произведения:
Модули градиентов:
Скалярное произведение градиентов:
Косинус искомого угла:
Отсюда искомый угол:
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: Саффка2004
Предмет: Русский язык,
автор: julia100187
Предмет: Химия,
автор: Аноним
Предмет: Русский язык,
автор: mysya4