ПОМОГИТЕ СРОЧНО ДАЮ 100 БАЛЛОВ
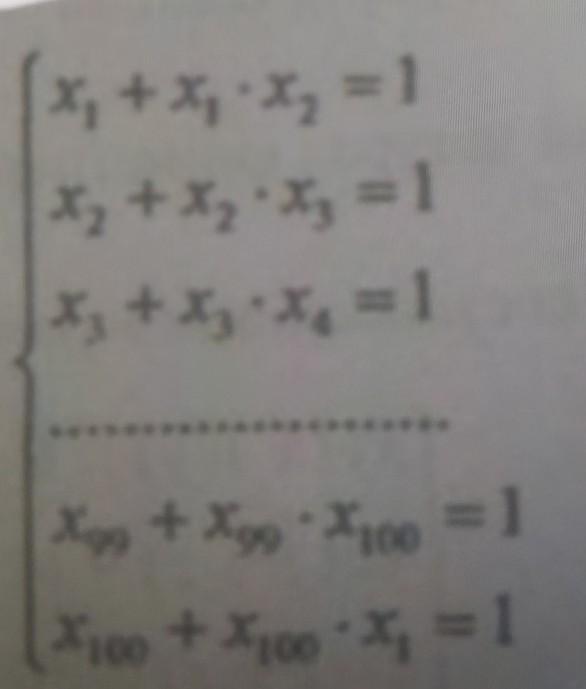
Ответы
Первоначальное соображение. Если т о для нахождения общего значения для всех иксов мы получаем уравнение
(мне показалось, или здесь пахнет золотым сечением?). Я постараюсь доказать, что других решений, кроме найденных двух, нет.
Рассмотрим функцию Из первого уравнения мы видим, что
из второго - что
Когда перейдем к сотому x, он будет получаться из первого 99-кратным применением функции, а последнее уравнение говорит о том, что первый икс выражается через первый икс 100-кратным применением функции. Докажем, что такое может быть только в двух случаях, которые уже были описаны выше, то есть когда f(x)=x. Все Вы знаете график функции f(x) - это стандартный школьный график гиперболы, опущенный на 1 вниз. Он состоит из двух ветвей - двух участков убывания. Сразу отсекаем случай, когда x>1, поскольку в этом случае f(x)<0, а тогда f(f(x))<0, и так далее, и мы к x никогда не вернемся. Не устраивает нас и x=1, так как f(1)=0, и мы не можем найти f(f(1)).
Пусть x>0 (но < 1) (кстати. лежит в этих пределах. Если
то в силу убывания функции
причем если f(x)>1, то на следующем этапе мы перескочим в отрицательные числа и в положительные никогда не вернемся. Также ничего хорошего не будет, если f(x)=1. Если же f(x)<1, то
Повторяя рассуждения, мы видим, что или мы на некотором этапе получаем отрицательное число и из отрицательных чисел уже не выберемся, или получим 1 и процесс на следующем этапе прекратится, или же мы будем перемещаться из положения правее
в положение левее
, затем снова правее, и так далее. Если бы уравнений в нашей системе было бы нечетное число, мы бы уже сейчас кричали ура, поскольку начальное число и конечное были бы по разные стороны от
Наша ситуация сложнее, но не является безнадежной. Давайте обозначим f(f(x))=g(x), тогда речь идет о том, чтобы 50-кратное применение функции g возвращало нас в первоначальную точку. Однако
Поскольку x лежит от нуля до 1, g'(x)>1, поэтому, используя теорему Лагранжа, мы можем утверждать, что то есть использование функции g увеличивает расстояние до нулевого икса, что не позволяет через несколько этапов вернуться назад.
Пусть x<0, тогда применение функции f снова дает отрицательное число. Среди отрицательных чисел мы уже имеем решение
Снова рассматриваем функцию g(x)=f(f(x)), только на новом промежутке мы имеем 0<g'(x)<1. Это говорит то том, что
то есть теперь вернуться через 50 этапов в точку x невозможно по причине уменьшения расстояния до
Вывод. Система имеет два решения
и
Xi*(1+Xi+1)=1
Xi+1=(1/Xi)-1
Xi+1-X1=(1/Xi)-1-Xi
Легко видеть Х100=Х1
Положим Xi+1-X1=0
Получаем Х^2-X=1
X=0,5*(1+sqrt(5)) или X=0,5*(1-sqrt(5))
Если положить все Хi=Х получаем решение.