Предмет: Математика,
автор: Ivanyato
Решите 5 пожалуйста!!
Приложения:
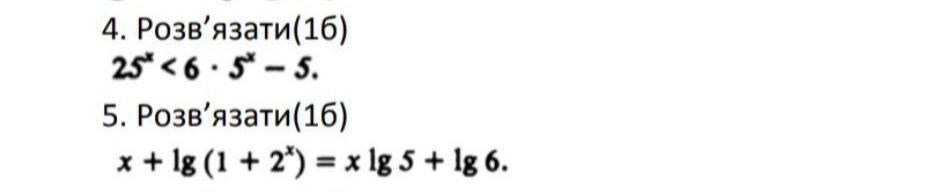
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
4)
5)
разделим обе части на
нет решений
О т в е т : x = 1
Похожие вопросы
Предмет: Английский язык,
автор: anchut35
Предмет: Русский язык,
автор: антошка9
Предмет: Русский язык,
автор: fnbiufhnjfk
Предмет: Химия,
автор: vladbrovkin2003