Помогите найти корни уравнения на промежутке. См.фото. Прошу рассписать все подробно,откуда корни,как они появились.
Правильные корни: -3п/2; п/2; -7п/6; п/6
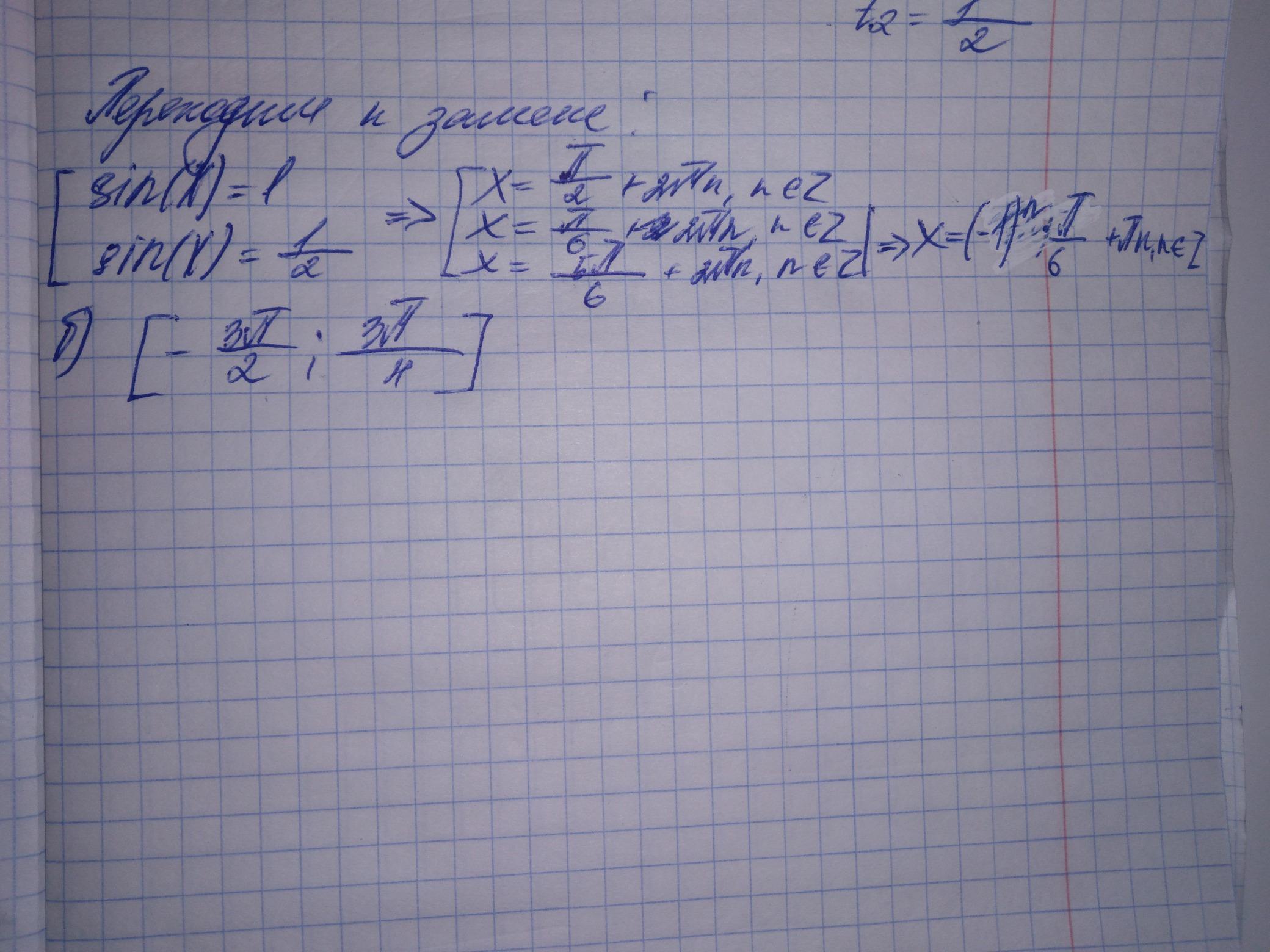
Ответы
Объяснение:
Тут при нахождении корней если 2 способа решения я покажи все эти способы.
Итак 1-вый способ: Способ неравенства - подствляем все корни в наш промежуток;
И решаем неравенство через "n". Забегая в перед не буду подробно решать и сразу вырожу ответ неравенства:
, учитывая что n∈Z (n принадлежит множеству целых чисел) мы получим:
n={-1;0}
n=0
n={-1;0}
Подставляем нашим корням и упростим
Ответ: x={ -3π/2; π/2; π/6; -7π/6; 5π/6}
2-ой способ;
Учитывая что промежуток начинается с отрицательного вырожения мы начинаем с n=-1 и берем те конри которые попадают в промежуток
n=-1: x=-3π/2; x=-7π/6; x=-11π/6, но x=-11π/6 нам не подходит потомучто не попадает в промежуток!
n=0: x=π/2; x=π/6; x=5π/6
n=1: x=5π/2; x=13π/6; x=17π/6, но при n=1 мы видим что наши корни не попадают в промежуток и исключаем эти корни.
Ответ: x={ -3π/2; π/2; π/6; -7π/6; 5π/6}
Вывод. У всех разный вкус. Некоторым нравится 1-вый способ, а некоторым 2-ой. Мне лично нравится 2-ой, так как этот способ не отнимает много времени и сразу выводит корни.