Предмет: Математика,
автор: sedgawer
Упростить выражение
Приложения:
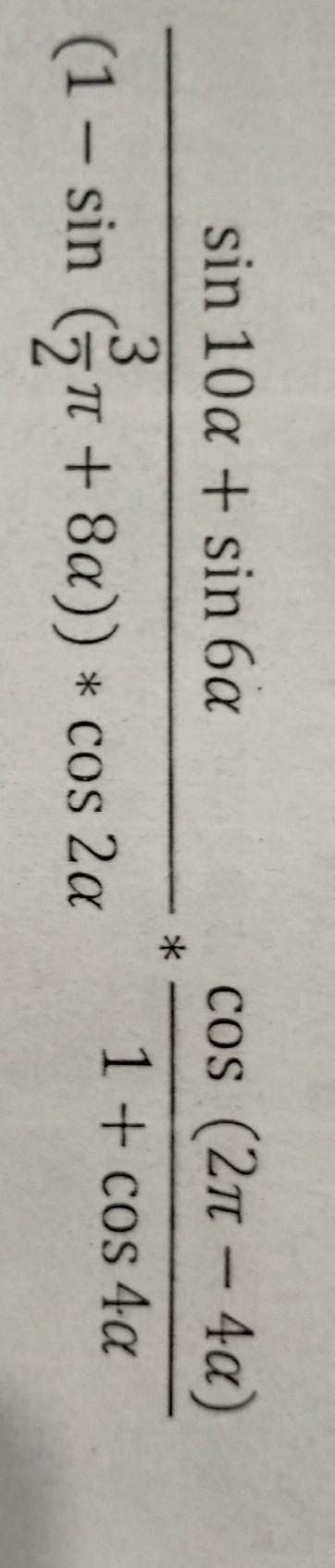
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
Для решения использованы формулы суммы синусов, формулы приведения, формулы синуса и косинуса двойного угла, формула тангенса угла.
Похожие вопросы
Предмет: Русский язык,
автор: Katyа05
Предмет: Русский язык,
автор: Аноним
Предмет: Французский язык,
автор: sveteni
Предмет: Обществознание,
автор: орочка1