Предмет: Математика,
автор: cris2020
вычислить определённый интеграл с точностью 0,001, разложив подынтегральную функцию в степенной ряд и проинтегрировав его почленно.
ИСПОЛЬЗУЯ ФОРМУЛУ “sinx=...”
Приложения:
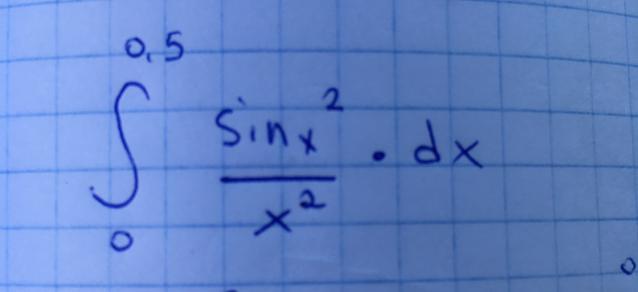
Ответы
Автор ответа:
1
Ответ:
≈ 929/960
Пошаговое объяснение:
Разложение синуса в ряд:
sin x = x - x^3/3! + x^5/5! - x^7/7! + ...
sin x^2 = x^2 - x^6/6 + x^10/120 - x^14/5040 + ...
Int(0;1) sin (x^2) / x^2 dx =
= Int(0;1) (x^2/x^2 - x^6/(6x^2) + x^10/(120x^2) - x^14/(5040x^2) ) dx =
= Int(0;1) (1 - x^4/6 + x^8/120 - x^12/5040) dx =
= x - x^5/30 + x^9/960 - x^13/65520 | (0;1) = A
У нас точность 0,001 = 1/1000, поэтому последний член можно не считать.
A = 1 - 1/30 + 1/960 - 0 + 0 - 0 = (960-32+1)/960 = 929/960
И можно узнать, как мы получаем в заменители это числа «6, 120, 5040»
Похожие вопросы
Предмет: Русский язык,
автор: rus302
Предмет: Окружающий мир,
автор: Аноним
Предмет: Русский язык,
автор: flyighter
Предмет: Алгебра,
автор: Gabriel313Novak
Предмет: История,
автор: аокисаттосьпаоч
“int(0;1)”