Question

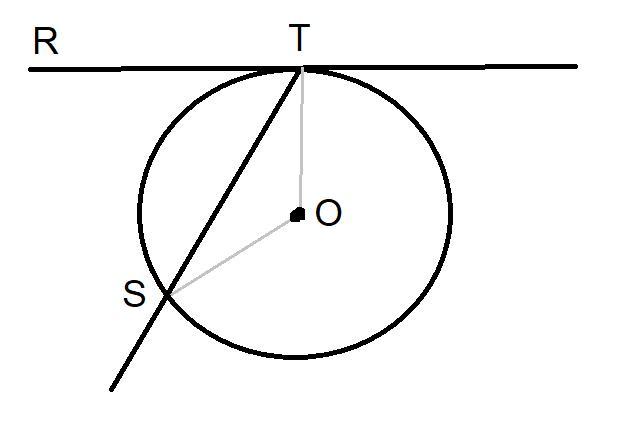
Найдите угол между касательной RT и хордой ST, проведенным из точки касания, если дуга ST равна 122°, а точка O - центр окружности.

Answer 1

Ответ:

61°

Объяснение:

Тут всё элементарно)))

Рассмотрим треугольник SOT, который образован из-за радиусов. Этот треугольник будет равнобедренный, так как радиусы окружности равны.

Угол SOT=дуге SТ=122°, так как центральный угол равен градусной мере дуги, на которую он опирается.

Найдём сумму углов при основании треугольника SOT.

Угол STO+угол OST=180°-122°=58°

Найдём отдельно углы при основании.

Угол STO=углу OST=58°:2=29°

Угол RTO=90°, так как касательная перпендикулярна к радиусу.

Угол RTS=угол RTO-угол STO.

Угол RTS=90°-29°=61°