Question

Полная поверхность 72 корень 3 см в квадрате. Найдите ребро октаэдра и его высоту

Answer 1

Ответ:

Ребро октаэдра = 6 cm

Высота октаэдра $=6\sqrt{2}cm$

Объяснение:

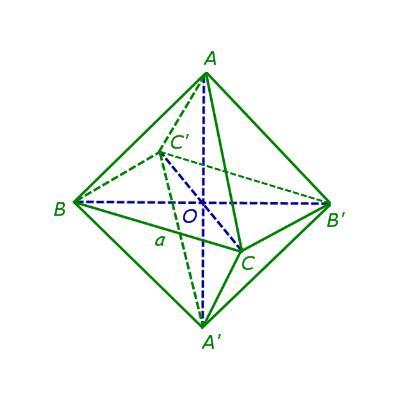
Предположим что речь идёт о правильном октаэдре. Тогда его грани - это восемь равносторонних треугольников (см. рисунок).

⇒ площадь одной грани (равностороннего треугольника) $=\frac{72\sqrt{3}}{8} = 9\sqrt{3} cm^{2}$

Т.к. площадь одной грани это площадь равностороннего треугольника, углы которого равны между собой, и равны 60° ⇒ есть такая формула площади треугольника:

$S=\frac{1}{2}*a*b*sin(alfa)$ - где a, b — стороны, alfa — угол между ними.

Т.к. наш треугольник равносторонний ⇒ a = b, a alfa = 60°, то подставив имеющиеся значения получим:

$9\sqrt{3} = \frac{1}{2} a^{2} sin(60)\\\\ 9\sqrt{3} = \frac{1}{2} a^{2} \frac{\sqrt{3}}{2} \\\\ 9\sqrt{3} = \frac{a^{2} \sqrt{3}}{4}\\\\ a^{2} \sqrt{3} = 4*9\sqrt{3}\\\\ a^{2}=\frac{36\sqrt{3}}{\sqrt{3}}\\\\ a^{2}=36\\\\ a = \sqrt{36}\\\\ a = 6 cm$

Рассмотрим фигуру BCB'C' - это квадрат образованный гранями a

⇒ диагональ квадрата вычисляется по формуле:

$BB' = CC'=a\sqrt{2} = 6\sqrt{2} cm$

⇒ $OC = OC' = OB = OB' = \frac{6\sqrt{2}}{2} =3\sqrt{2} cm$

Рассмотрим Δ AOC - это прямоугольный треугольник.

В нем:

$AC = a = 6 cm$ - это гипотенуза;

$OC = \frac{6\sqrt{2}}{2} cm$ - один из катетов.

По Теореме Пифагора:

$AC^{2} = AO^{2} + OC^{2} \\\\6^{2} = AO^{2} + (3\sqrt{2})^{2} \\\\ 36 = AO^{2} + (9*2)\\\\ AO^{2} = 36-18\\\\ AO = \sqrt{18} \\\\ AO = 3\sqrt{2} cm$

Т.к. наш октаэдр правильный ⇒ AO = OA'

⇒ высота октаэдра:

$AA' = 2 * AO\\\\AA' = 2*3\sqrt{2}\\\\AA' = 6\sqrt{2}cm$