Предмет: Алгебра,
автор: minandkim
Найдите область определения функции.

Ответы
Автор ответа:
1
Решение задания прилагаю
Приложения:

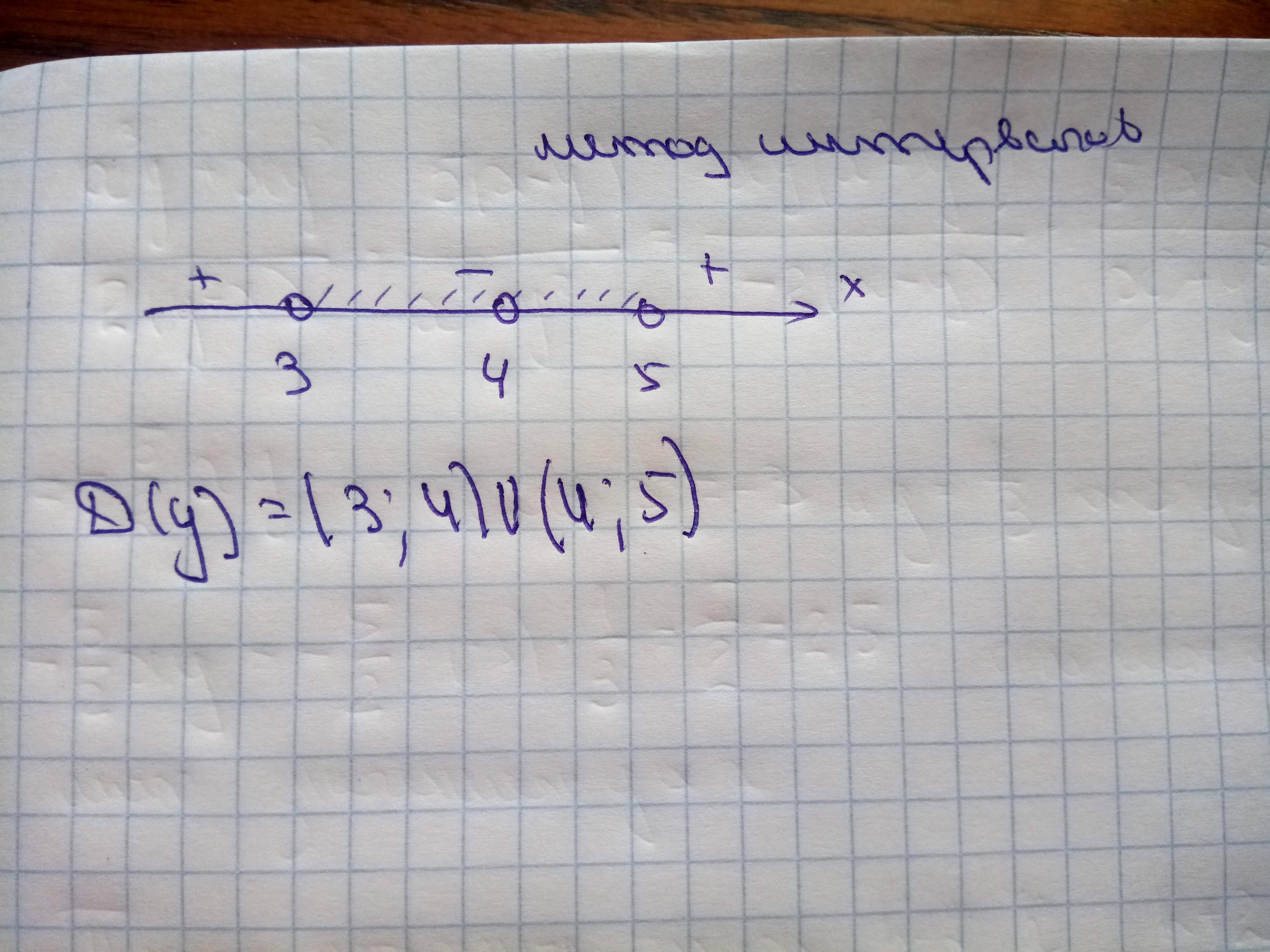
Автор ответа:
0
+ - +
_____₀_____₀_____
3 5
/////////////
x ∈ (3 ; 5)
Объединив оба ограничения , получим окончательный ответ :
x ∈ (3 ; 4) ∪ (4 ; 5)
Похожие вопросы
Предмет: Технология,
автор: 8675434
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: География,
автор: Harley171103