Предмет: Математика,
автор: raqzer113
Найти площадь длины ограниченной линиями y=x³ x=-2 x=2 через интеграл.
30 балов.
Ответы
Автор ответа:
1
Пошаговое объяснение:
Шаг 1: находим координаты х точек перечечения графиков y=x^2+1 и y=-x+3.
x^2+1 = -x+3; x^2+x-2 = 0; x1 = -2; x2 = 1.
Шаг 2: Находим определенный интеграл функции y = -x+3 в пределах от -2 до 1.
Первообразная этой функции будет Y = -1/2*x^2 + 3x + С
Подставляя пределы интегрирования получаем площадь под функцией S1 = -1/2 + 3 + 2 + 6 = 10,5.
Шаг 3: Находим определенный интеграл функции y = x^2+1 в пределах от -2 до 1.
Первообразная этой функции будет Y = 1/3*x^3 + x + С
Подставляя пределы интегрирования получаем площадь под функцией S2 = 1/3 + 1 + 8/3 +2 = 6.
Шаг 4: S = S1-S2; S = 10,5-6; S = 4,5.
raqzer113:
Посмотри формулы
Там с 1 по 5 и попробуй решить
Сам
Через фотомачь такой же ответ если скоординировать под интеграл
А если по правильному то там не такое длинное
По решению
График сложный чертить разве что
Если есть функция сфоткать и переслать я мог бы график и решение без ответа написать и скинуть
там есть такая функция
Стесняюсь говорить, но х в кубе вообще-то симметрично относительно оси оу, как же вышли разные площади слева и справа?
Автор ответа:
1
Ответ: площадь фигуры, наверное. 8 кв единиц. См фото.
Пошаговое объяснение:
Приложения:
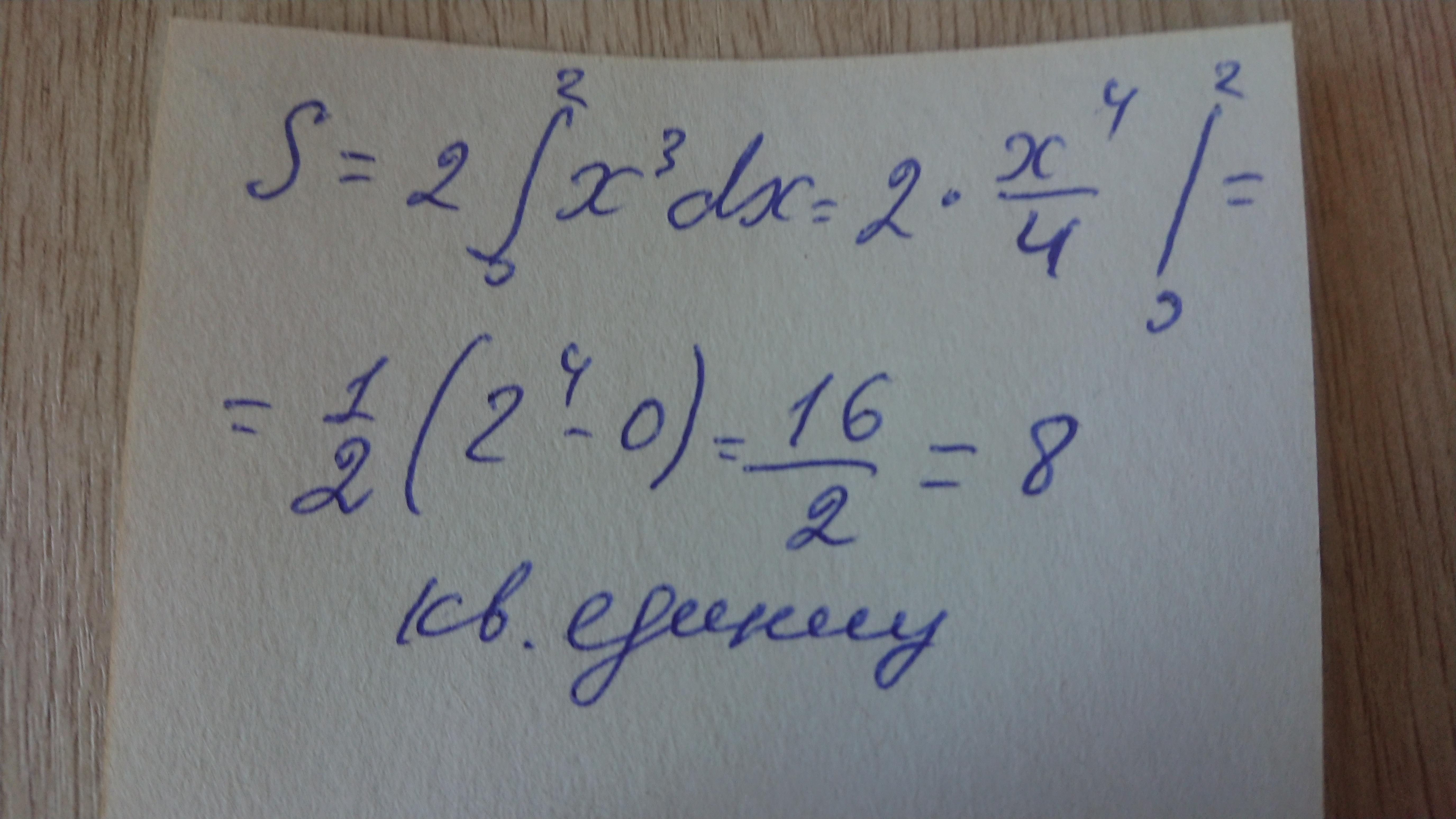
Правильно
Вот тут правильно
Если есть функция переслать фото сюда скажи пожалуйста я график скину сюда
а ну такой функции к сож.нет:(
Есть Раздиление интегральная функция и функция. Это как различия высшая математика и средняя математика.
Скупая похвала)))
Похожие вопросы
Предмет: Русский язык,
автор: Zamilia
Предмет: Другие предметы,
автор: 777GELENDVAGEN777
Предмет: Українська література,
автор: yulia200122
Предмет: Қазақ тiлi,
автор: prinsessa0609
Предмет: Русский язык,
автор: Arcator