Найти наибольшее значение функции и найти наименьшее значение функции
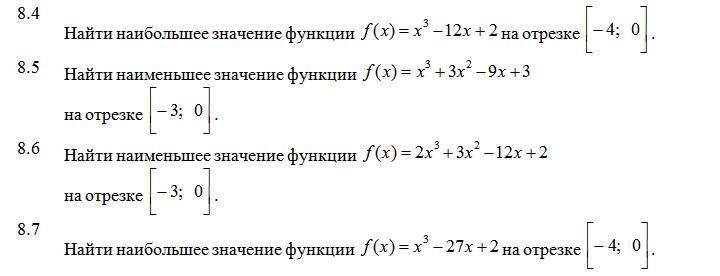
Ответы
Ответ:
Пошаговое объяснение:
8.4.
f(x)=x³-12x+2; [-4; 0]
f'(x)=3x²-12
3x²-12=0 |3
x²-4=0; x²=4; x=±√4
x₁=-2; x₁∈[-4; 0]
x₂=2; x₂∉[-4; 0]
f(-4)=(-4)³-12·(-4)+2=-64+48+2=-14
f(-2)=(-2)³-12·(-2)+2=-8+24+2=18
f(0)=0³-12·0+2=2
Ответ: наибольшее значение M=18, наименьшее значение m=-14.
8.5.
f(x)=x³+3x²-9x+3; [-3; 0]
f'(x)=3x²+6x-9
3x²+6x-9=0 |3
x²+2x-3=0; D=4+12=16
x₁=(-2-4)/2=-6/2=-3; x₁∈[-3; 0]
x₂=(-2+4)/2=2/2=1; x₂∉[-3; 0]
f(-3)=(-3)³+3·(-3)²-9·(-3)+3=-27+27+27+3=30
f(0)=0³+3·0²-9·0+3=3
Ответ: наибольшее значение M=30, наименьшее значение m=3.
8.6.
f(x)=2x³+3x²-12x+2; [-3; 0]
f'(x)=6x²+6x-12
6x²+6x-12=0 |6
x²+x-2=0; D=1+8=9
x₁=(-1-3)/2=-4/2=-2; x₁∈[-3; 0]
x₂=(-1+3)/2=2/2=1; x₂∉[-3; 0]
f(-3)=2·(-3)³+3·(-3)²-12·(-3)+2=-54+27+36+2=11
f(-2)=2·(-2)³+3·(-2)²-12·(-2)+2=-16+12+24+2=22
f(0)=2·0³+3·0²-12·0+2=2
Ответ: наибольшее значение M=22, наименьшее значение m=2.
8.7.
f(x)=x³-27x+2; [-4; 0]
f'(x)=3x²-27
3x²-27=0 |3
x²-9=0; x²=9; x=±√9
x₁=-3; x₁∈[-4; 0]
x₂=3; x₂∉[-4; 0]
f(-4)=(-4)³-27·(-4)+2=-64+108+2=46
f(-3)=(-3)³-27·(-3)+2=-27+81+2=56
f(0)=0³-27·0+2=2
Ответ: наибольшее значение M=56, наименьшее значение m=2.