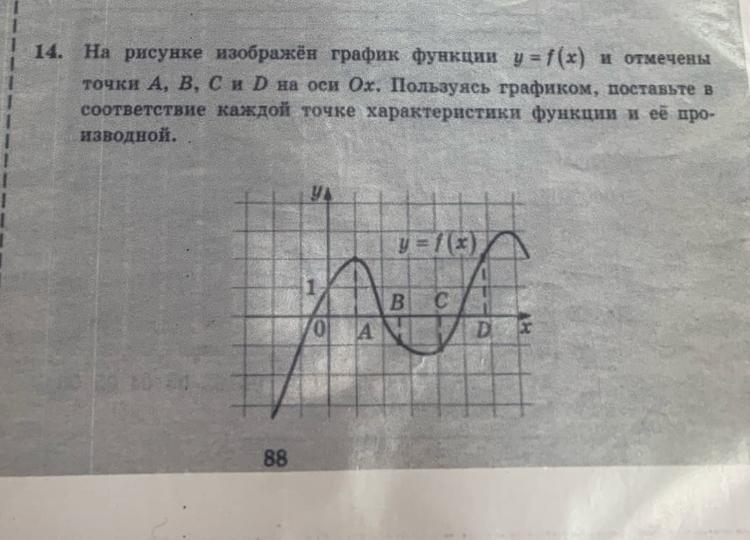
На рисунке изображён график функции и отмечены точки а б в и на ох оси
Пользуясь графиком, поставьте в соответствие каждой точке характеристики функции и её производной.
Очень срочно
Хотелось бы подробно что бы расписали ❤️

Ответы
Ответ:
4132
Пошаговое объяснение:
Рассмотрим каждую точку.
А) Точка А (1; 2)
При х = 1 значение функции положительно (у = + 2).
Если провести касательную к данному графику в точке А (1; 2), то она будет параллельна оси Ох, а это значит, значение производной функции в точке А (1; 2) равно нулю (у' = 0).
Ответ: 4
Б) Точка В (2,5; -1)
При х = 2,5 значение функции отрицательно (у = -1).
Если взять на оси Ох точку минимально правее точки В, например, х = 3, то при х = 3 у будет равен ≈ -1,1, то есть функция будет убывать, а это значит, что значение производной функции в анализируемой точке В (2,5; -1) отрицательно (у' < 0).
Ответ: 1
В) Точка С ( 4; - 1,2)
При х = 4 значение функции отрицательно ( у = -1,2).
Если взять на оси Ох точку минимально правее точки С, например, х = 4,1, то при х = 4,1 у будет равен ≈ - 1, то есть функция будет возрастать, а это значит, что значение производной в анализируемой точке С (4; -1,2) положительно (у' > 0).
Ответ: 3.
Г) Точка D (5,9; 2)
При х = 5,9 значение функции положительно ( у = 2).
Если взять на оси Ох точку минимально правее точки D, например, х = 6, то при х = 6 у будет равен ≈ 2,2, то есть функция будет возрастать, а это значит, что значение производной в анализируемой точке D (5,9; 2) положительно (у' > 0).
Ответ: 2
Общий ответ: 4132