Question

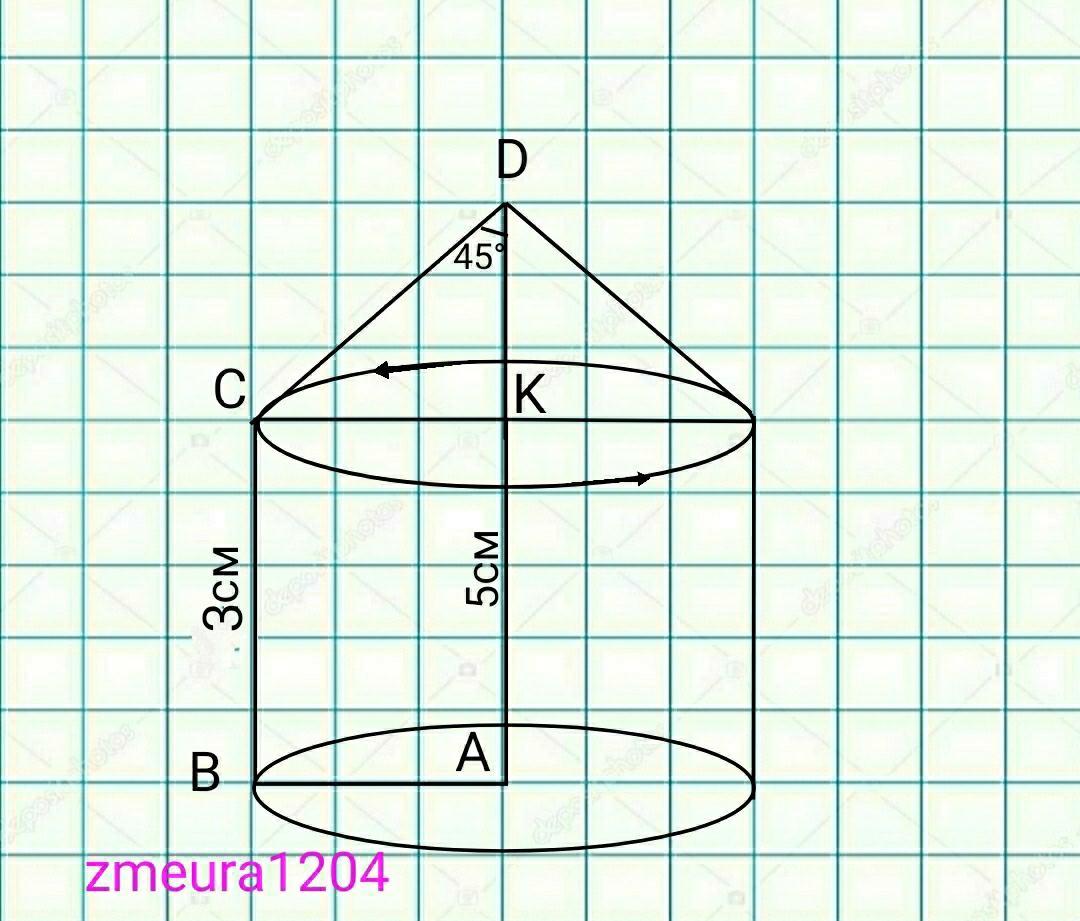
Прямоугольная трапеция с углом в 45° вращается вокруг прямой, содержащей большее основание. Найдите площадь поверхности тела вращения, если основания трапеции равны 3 и 5.​

Answer 1

Ответ:

16π+4√2 см²

Пошаговое объяснение:

CB=AK=3см

КD=AD-AK=5-3=2см

∆СKD- прямоугольный равнобедренный треугольник

(<СКD=90°; <CDK=45°; <DCK=45°) углы при основании равны. СК=KD=2см

По теореме Пифагора

СD=√(CK²+KD²)=√(2²+2²)=2√2 см

СК=ВА=2см.

При вращении получили конус и цилиндр с равным радиусом

R=CK=BA=2см

Sбок.к.=πRL=π*CK*CD=π*2*2√2=4√2π см² площадь боковой поверхности конуса

Sбок.ц=2πRh=2π*BA*BC=2π*2*3=12π см² площадь боковой поверхности цилиндра.

Sосн.ц=πR²=π*2²=4π см² площадь основания цилиндра.

Sз.ф.=Sбок.к+Sбок.ц+Sосн.ц=

=4√2π+12π+4π=16π+4√2π см² площадь заданной фигуры.