Предмет: Математика,
автор: УченикУченица
Необходимо разрешить неопределенность и вычислить значение предела функции. Помогите, пожалуйста
Приложения:
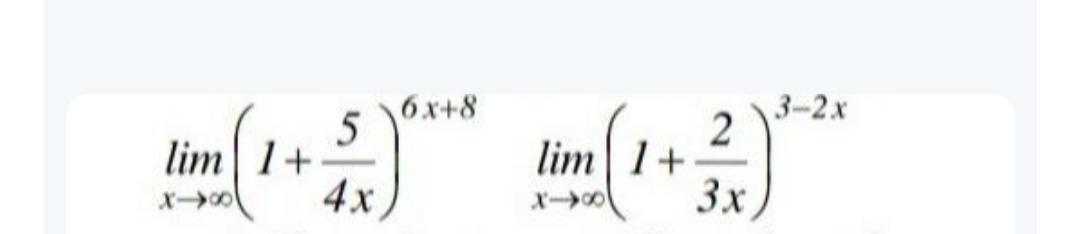
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Українська література,
автор: pkali9nD6ekAnnO
Предмет: Русский язык,
автор: SuperMaxi2312
Предмет: Русский язык,
автор: bibka2
Предмет: Математика,
автор: Demитра13
Предмет: Математика,
автор: Timofey2190