Предмет: Алгебра,
автор: Аноним
Помогите решить срочно, прошу!!!!!! Дам 50 баллов
Вариант 1
Приложения:
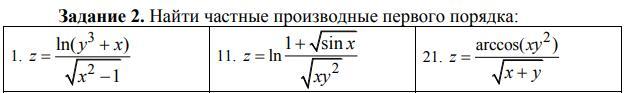
Ответы
Автор ответа:
0
Ответ:
1.
2.
3.
Похожие вопросы
Предмет: Английский язык,
автор: алещаг
Предмет: Қазақ тiлi,
автор: Дракон100000
Предмет: Английский язык,
автор: cemnet
Предмет: Обществознание,
автор: Аноним