Предмет: Математика,
автор: dipseydipsey
50 баллов. найти производную dy/dx
Приложения:
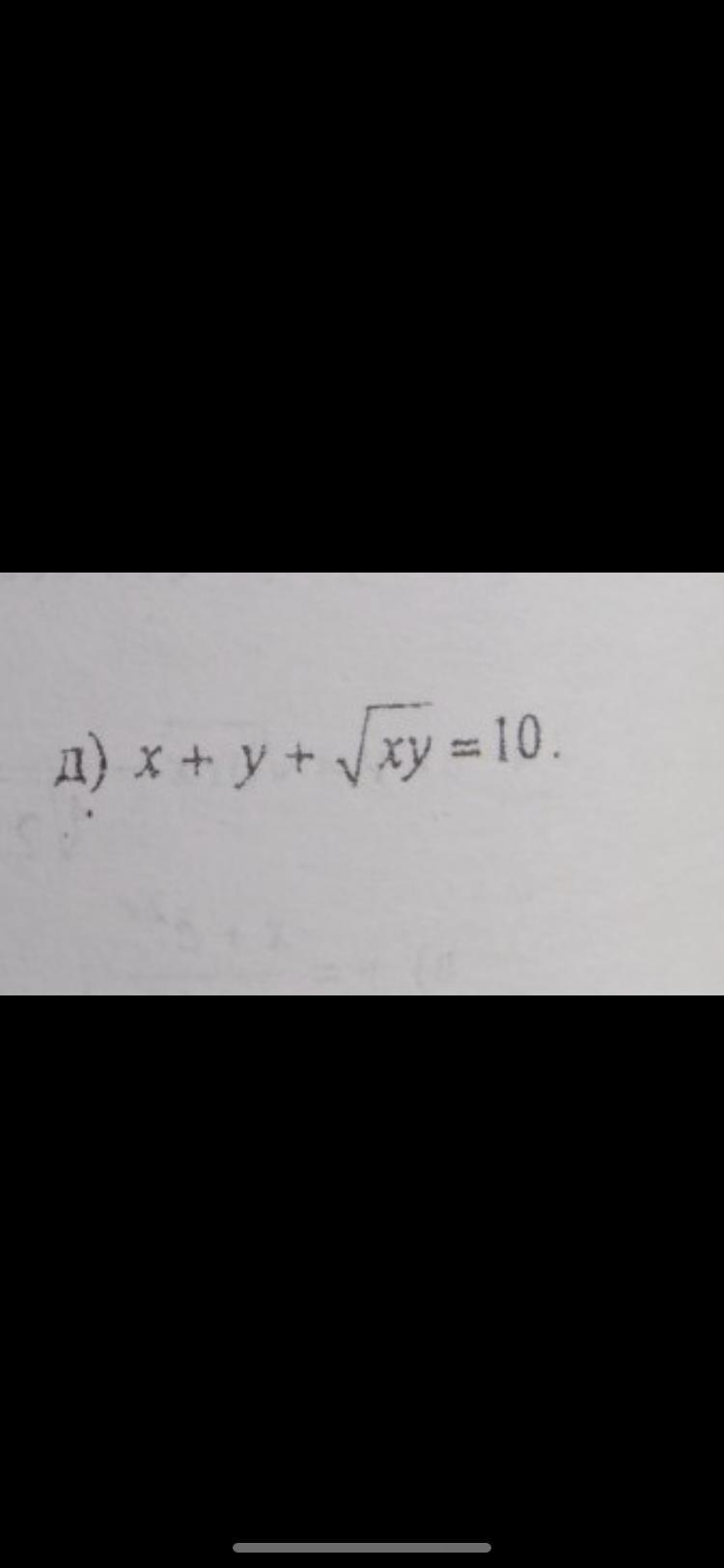
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: mamakreed
Предмет: Английский язык,
автор: Аноним
Предмет: Английский язык,
автор: Linabelokurski
Предмет: Русский язык,
автор: X3kak17
Предмет: Русский язык,
автор: lemyrrrrr12345