Предмет: Математика,
автор: gledsosnicov
Дан прямоугольник со сторонами 3 и 4см, в точке пересечения диагоналей прямоугольника восстановлен перпендикуляр к плоскости прямоугольника, длина которого 7см. Найти расстояние от вершины перпендикуляра до вершин прямоугольника. С РИСУНКОМ И ДАНО
Ответы
Автор ответа:
6
Ответ:
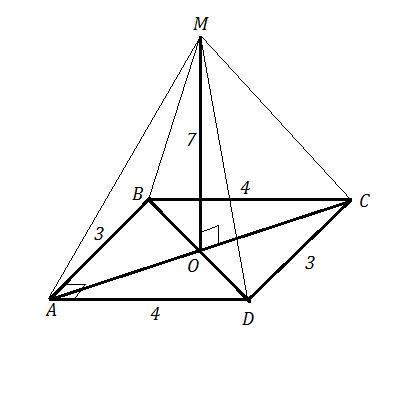
Дано: АВСD - прямоугольник , АВ=CD=3 см , AD=BC=4 см ,
MO⊥ABCD ⇒ MO⊥AC и MO⊥BD .
Найти: AM , BM , CM , DM .
AC=BD=√(3²+4²)=√25=5 см , AО=BO=CO=DO=5^2=2,5 см .
Из ΔАОМ: ∠АОМ=90° , AM=√(7²+2,5²)=√55,25≈7,43 cм
Так как ΔАОМ=ΔBOM=ΔCOM=ΔDOM по двум катетам, то
AM=BM=CM=DМ=√55,25≈7,43 см .
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Alexsyulecia
Предмет: Русский язык,
автор: Nastyz11
Предмет: Другие предметы,
автор: котя355
Предмет: Математика,
автор: тося30
Предмет: Русский язык,
автор: РомаЛСП