Предмет: Математика,
автор: zhoramitin03
Решите дифференциальное уравнение! Срочно ребят, любое!
Приложения:
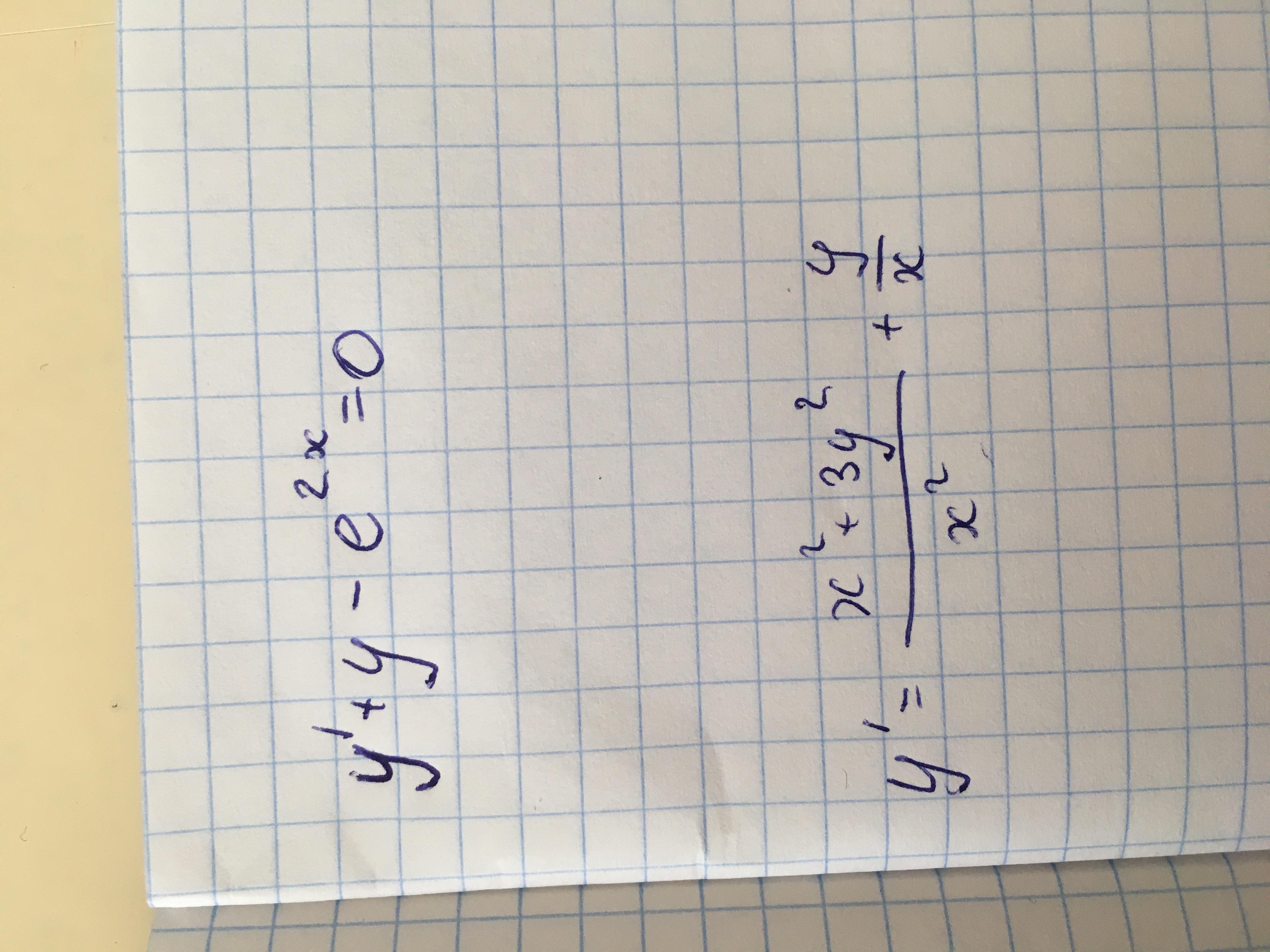
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Другие предметы,
автор: KatexPysia
Предмет: Английский язык,
автор: yayrolika
Предмет: Другие предметы,
автор: КотВасёк
Предмет: Химия,
автор: anzhela247
Предмет: Информатика,
автор: mosux1