Предмет: Геометрия,
автор: fewffq
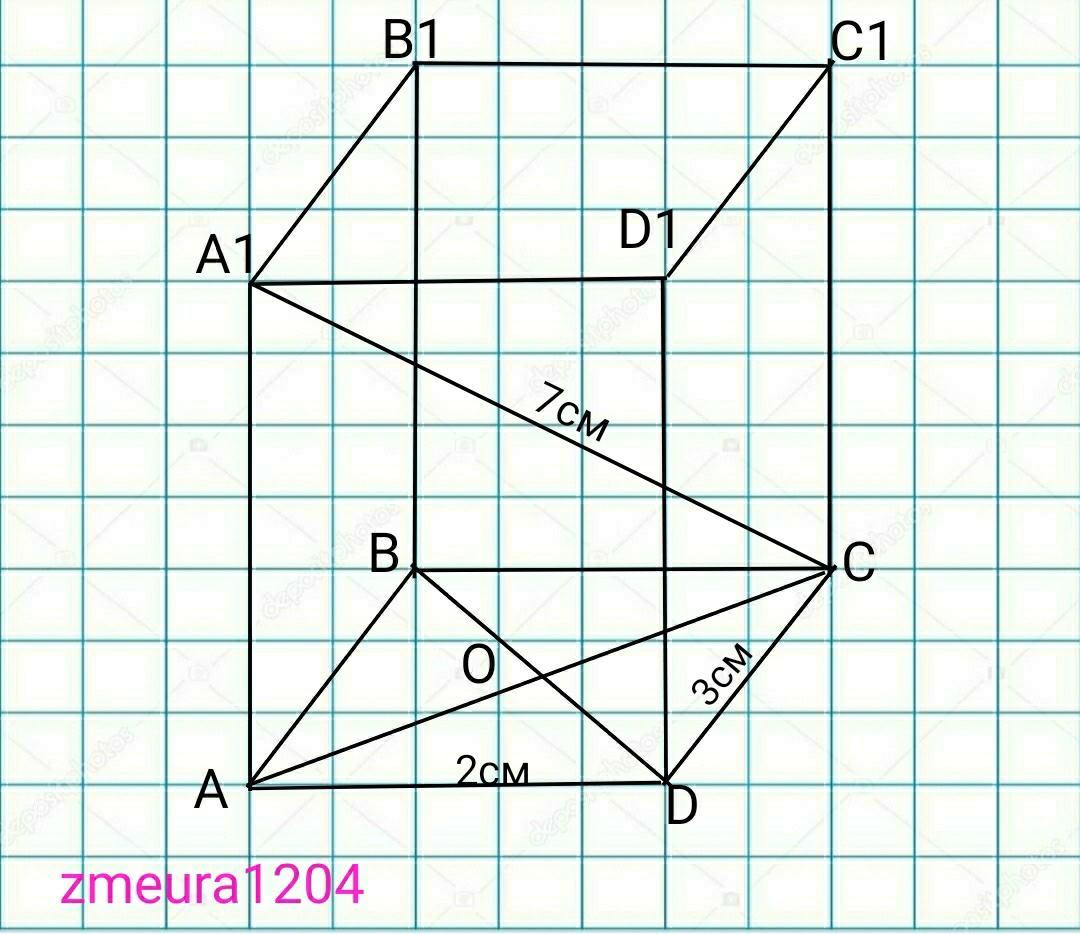
Вычислите площадь полной поверхности прямоугольного параллелепипеда, длины сторон основания которого 2 см и 3 см, а диагональ параллелепипеда 7 см.
Ответы
Автор ответа:
1
Ответ:
72см²
Объяснение:
∆АСD- прямоугольный треугольник.
По теореме Пифагора
АС=√(АD²+DC²)=√(3²+2²)=√(9+4)=√13 см
∆АА1С- прямоугольный треугольник
По теореме Пифагора
АА1=√(А1С ²-АС²)=√(7²-(√13)²)=√(49-13)=
=√36=6см высота призмы
Sбок=2(АD+DC)*AA1=2(3+2)*6=60см²
Sпол=2*(АD*DC)+Sбок=2*2*3+60=
=12+60=72см²
Приложения:
Автор ответа:
1
по двум ребрам основания найдем диагональ основания по Пифагору.
√(2²+3²)=√13, по диагонали параллелепипеда и основания найдем третье ребро параллелепипеда. √(49-13)=6
тогда площадь полной поверхности равна 2*(2*3+2*6+3*6)=72
Ответ 72см²
Аноним:
√13 это не третье ребро это диагональ основания.
Извините, протупила.
Похожие вопросы
Предмет: Русский язык,
автор: shehireva
Предмет: Русский язык,
автор: titorenckolyud
Предмет: Русский язык,
автор: Аноним
Предмет: Физика,
автор: marta198603
Предмет: Математика,
автор: pav97322p77ug4