Question

решите задачу пожалуйста, завтра контрольная​

Answer 1

Ответ:

MD = 2,5 см

Объяснение:

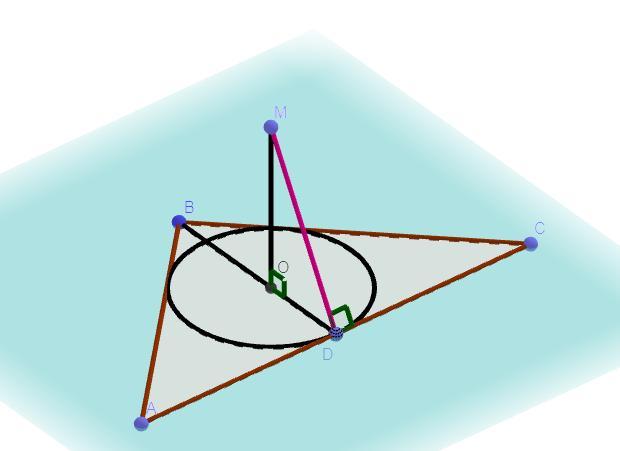
Дано: AC = 6 см, AB = BC = 5 см, О - центр вписаного кола, OM ⊥ ABC,

OM = 2 см, MD ⊥ AC.

Знайти: MD - ?

Розв'язання: За теоремою про три перпендикуляри так як OM ⊥ ABC,

MD ⊥ AC, тоді OD ⊥ AC, отже OD - радіус вписаного кола, так як радіус вписаного кола проведений з центра кола до сторони трикутника і перпендикулярний до сторони. Нехай півпериметр трикутника p, тоді

p = 0,5 * PΔABC = 0,5(AB + BC + AC) = 0,5(5 + 5 + 6) = 0,5 * 16 = 8 см.

За формулами площі триутника слідує наступне:

$\sqrt{p(p - AB)(p - BC)(p - AC)} = p*OD$

$OD = \frac{\sqrt{p(p - AB)(p - BC)(p - AC)} }{p} = \frac{\sqrt{8(8 - 5)(8 - 5)(8 - 6)} }{8} = \frac{\sqrt{8 * 3 * 3 * 2} }{8} = \frac{12}{8} = 1,5$ см.

Розглянемо трикутник ΔMOD. За теоремою Піфагора:

$MD = \sqrt{MO^{2} + OD^{2} } = \sqrt{2^{2} + 1,5^{2} } = \sqrt{4 + 2,25} = \sqrt{6,25} = 2,5$ см.