Предмет: Геометрия,
автор: Irina216816
Даю 50 балов!!!!!!!!!!!!!
Найдите длину окружности, вписанной в квадрат, и площадь круга, описанного около него, если сторона квадрата равна 4.
Ответы
Автор ответа:
0
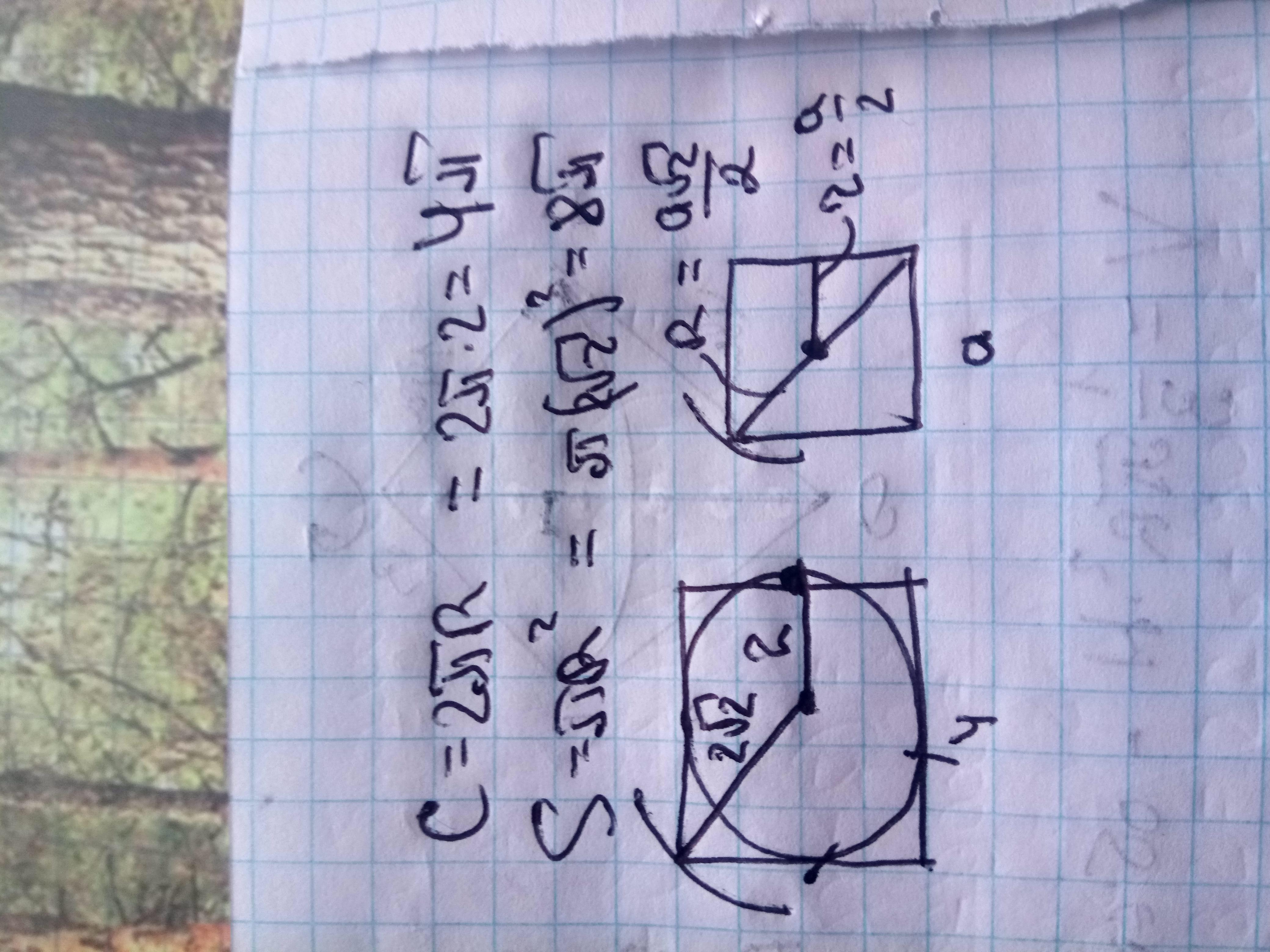
Решение задания прилагаю
Приложения:
Автор ответа:
0
Ответ:
C = 12,56 см
S = 25,12 см²
Объяснение:
- формула длины вписанной окружности
- формула площади описанного круга
- формула диагонали квадрата
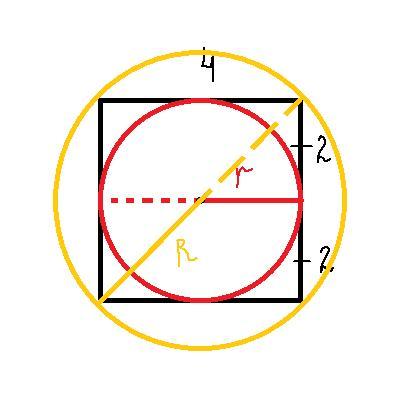
Из рисунка видно, что радиус вписанной окружности равен половине стороны квадрата, т.е. двум сантиметрам, значит
≈ 12,56 см
Радиус описанного круга равен половине диагонали квадрата, значит
≈ 25,12 см²
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Kozlyakovaliza
Предмет: Русский язык,
автор: and170606
Предмет: Қазақ тiлi,
автор: dilnaz009
Предмет: Математика,
автор: knyashp782q1
Предмет: Қазақ тiлi,
автор: тараканчик1