Предмет: Алгебра,
автор: Good9luck
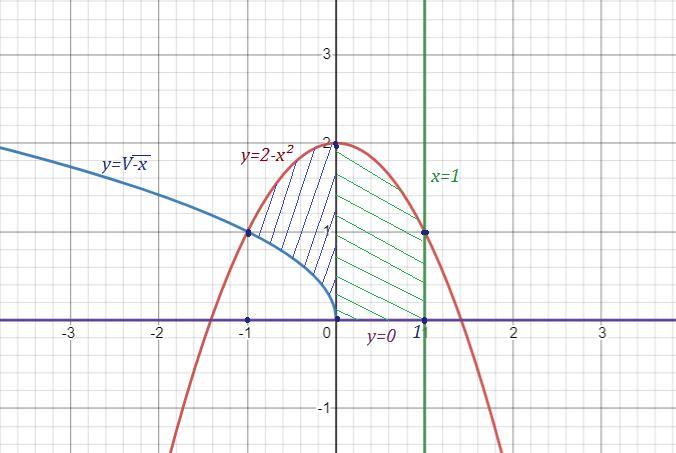
обчисліть площу фігури , обмеженої лініями:
у=корень из -х, у=2-х^2, х=1, у=0
Ответы
Автор ответа:
1
Ответ:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: Vahonin81
Предмет: Французский язык,
автор: ashxen1
Предмет: Русский язык,
автор: Мина5511
Предмет: Математика,
автор: Ricon1