Предмет: Алгебра,
автор: Аноним
Решите пожалуйста !!!!
Приложения:

Ответы
Автор ответа:
3
Ответ:
Приложения:
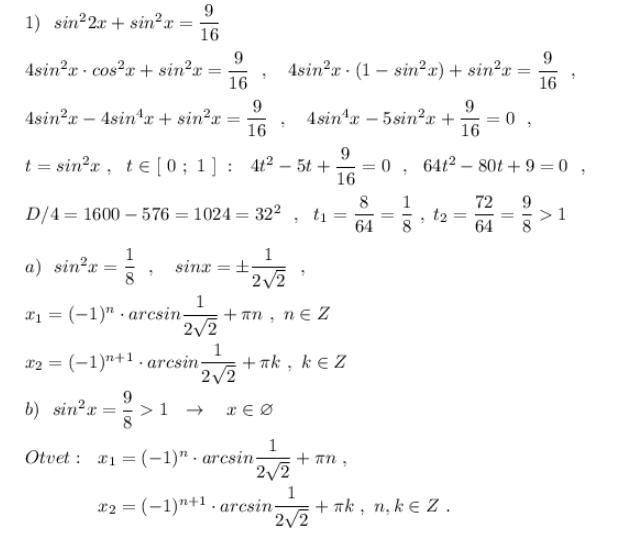
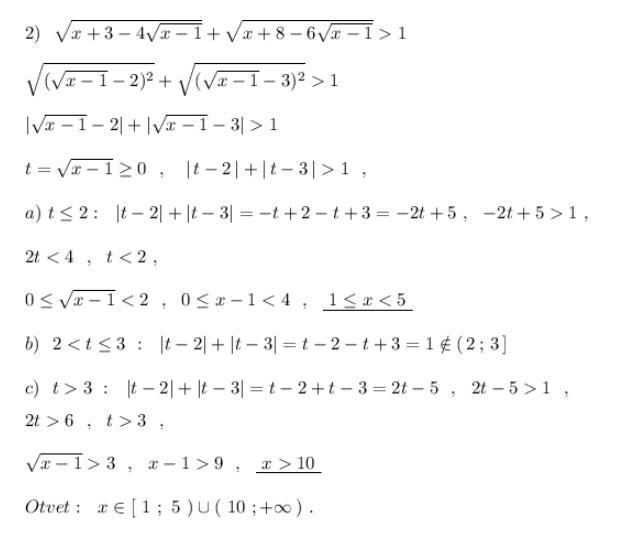
NNNLLL54:
да
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: Аноним
Предмет: Окружающий мир,
автор: Аноним
Предмет: Информатика,
автор: sizarlino
Предмет: Геометрия,
автор: dzhoxa