Question

Найдите максимальный объем многогранника с пятью вершинами, который можно поместить в шар радиуса 2√3.

Answer 1

Ответ:

V =√3/2 R^3 =√3/2 (2√3)^3 =36

Объяснение:

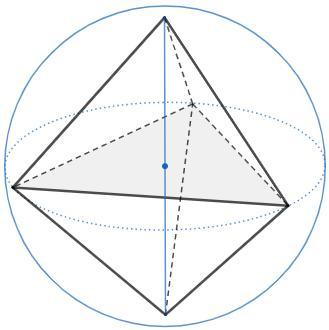
Представим многогранник как два тетраэдра с общим основанием.

Максимальная площадь основания - площадь правильного треугольника, вписанного в окружность R.

S =3√3/4 R^2

Максимальная суммарная высота тетраэдров 2R.

V =V1+V2 =1/3 S (h1+h2) =1/3 *3√3/4 R^2 *2R =√3/2 R^3