Найти наименьшее и наибольшее значение функции
f(x)= х^4-8х^2-9 на отрезке |0;3|
Ответы
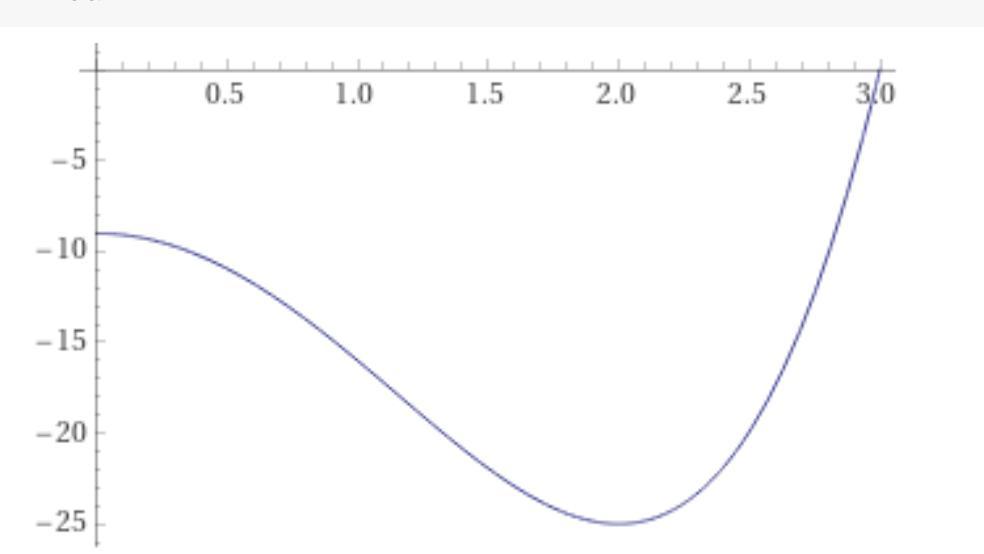
Ответ: Наименьшее: -25, наибольшее: 0
Пошаговое объяснение:
Рассмотрим крайние точки:
Получаем x=0, x=-2, x=2 - это крайние точки, где функция меняет свое направление.
При x∈ (-∞, -2) функция убывает
При x∈ (-2, 0) функция возрастает
При x∈ (0, 2) функция убывает
При x∈ (2, ∞) функция возрастает
Рассмотрим отрезок [0;3]. Функция убывает до x=2 и от нее же начинает возрастать. Тогда очевидно что при x=2 функция будет достигать своему минимума
Остается вопрос касательно максимальной значении функции. У нас тут на самом деле спор между 0 или 3, так как функция возрастает при x=3 и при x=0 она переходит от возрастания к убыванию и является локальным экстремумом для всех точек вблизи x=0. Попробуем вычислить .
Тогда наибольшее значение функции будет равно 0.
P.S. прикрепил как эта функция выглядит на x [0;3].
Решение задания прилагаю
