В треугольнике
BM=MC=6 см,
AM=10 см,
угол AMD=углу CMD,
DH перпендикулярен AM,
DH=3см
найдите площадь треугольника ABC
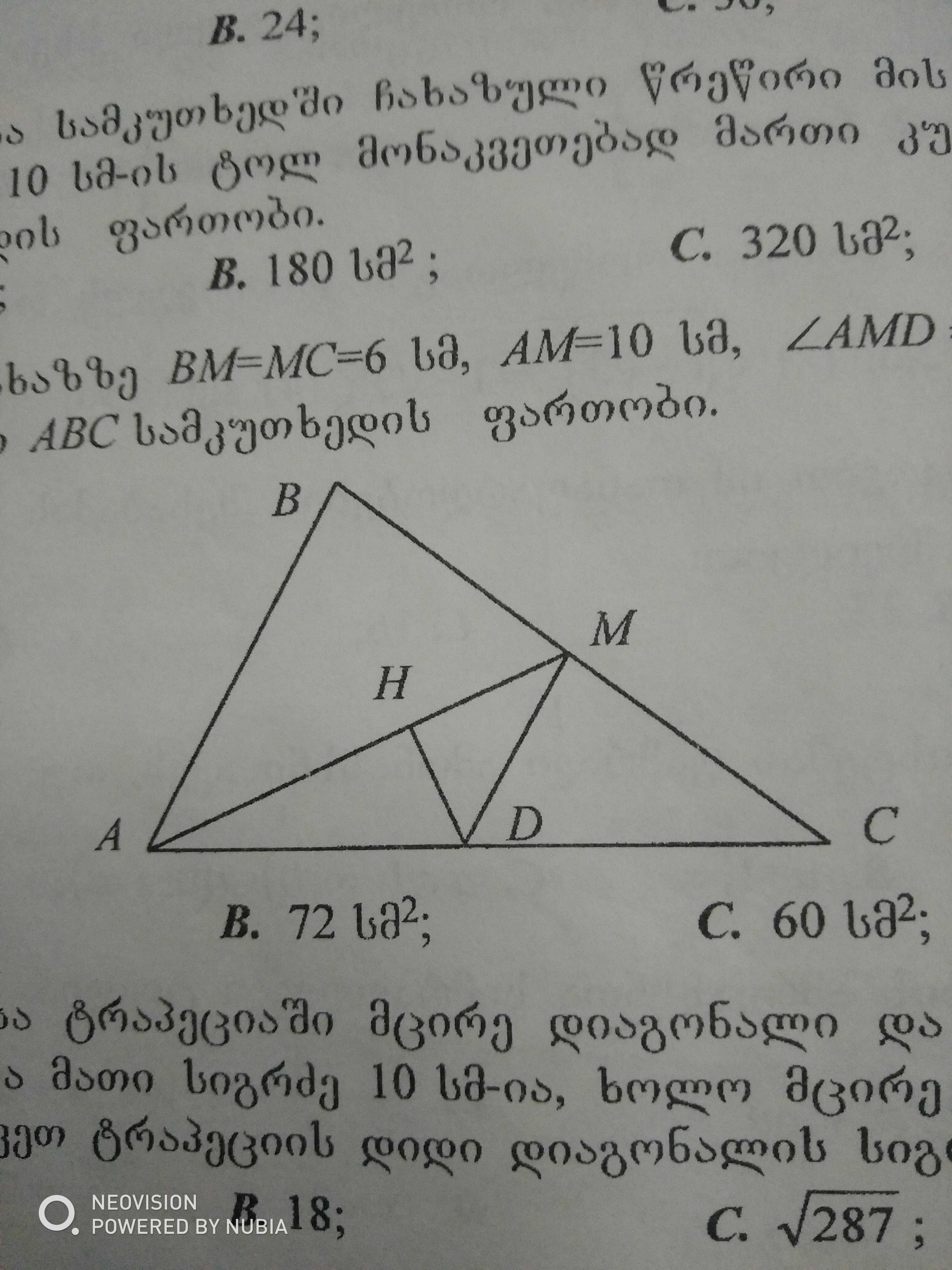
Ответы
Ответ:
48 см²
Пошаговое объяснение:
1) Теорема. Медиана треугольника делит его на два равновеликих треугольника. Так как, согласно условию задачи, ВМ = МС, то это значит, что АМ является медианой треугольника АВС, а площади треугольников АВМ и АМС равны между собой:
S ΔАВC = S ΔАВМ + S ΔАМС,
а так как S ΔАВМ = S ΔАМС, то
S ΔАВC = 2 · (S ΔАМС).
2) Площадь треугольника АМС равна сумме площадей треугольников АМD и MDC:
S ΔАМС = S ΔАМD + S ΔСMD
3) Согласно условию задачи, DH⊥AM, то есть DH является высотой треугольника АMD, проведённой к основанию АМ, следовательно, площадь треугольника АМD равна:
S ΔАМD = (АМ · DH) : 2 = 10 · 3 : 2 = 30 : 2 = 15 см².
4) Согласно условию задачи, ∠AMD треугольника АМD равен ∠CMD треугольника CMD. Следовательно, sin ∠АМD = sin ∠CМD, и тогда площади данных треугольников соответственно равны:
S ΔАМD = 0,5 · АМ · МD · sin ∠АМD, (1)
S ΔСMD = 0,5 · МС · МD · sin ∠АМD. (2)
Разделим (1) на (2), получим:
S ΔАМD : S ΔСMD = (0,5 · АМ · МD · sin ∠АМD) : (0,5 · МС · МD · sin ∠АМD)
S ΔАМD : S ΔСMD = AM : МС. (3)
Подставим в (3) известные значения и найдём S ΔСMD.
15 : S ΔСMD = 10 : 6
S ΔСMD = 15 · 6 : 10 = 90 : 10 = 9 см²
5) S ΔАМС = S ΔАМD + S ΔСMD = 15 + 9 = 24 см²
6) S ΔАВC = 2 · (S ΔАМС) = 2 · 24 = 48 см²
Ответ: S ΔАВC = 48 см²