ТЕРМІНОВО !!!
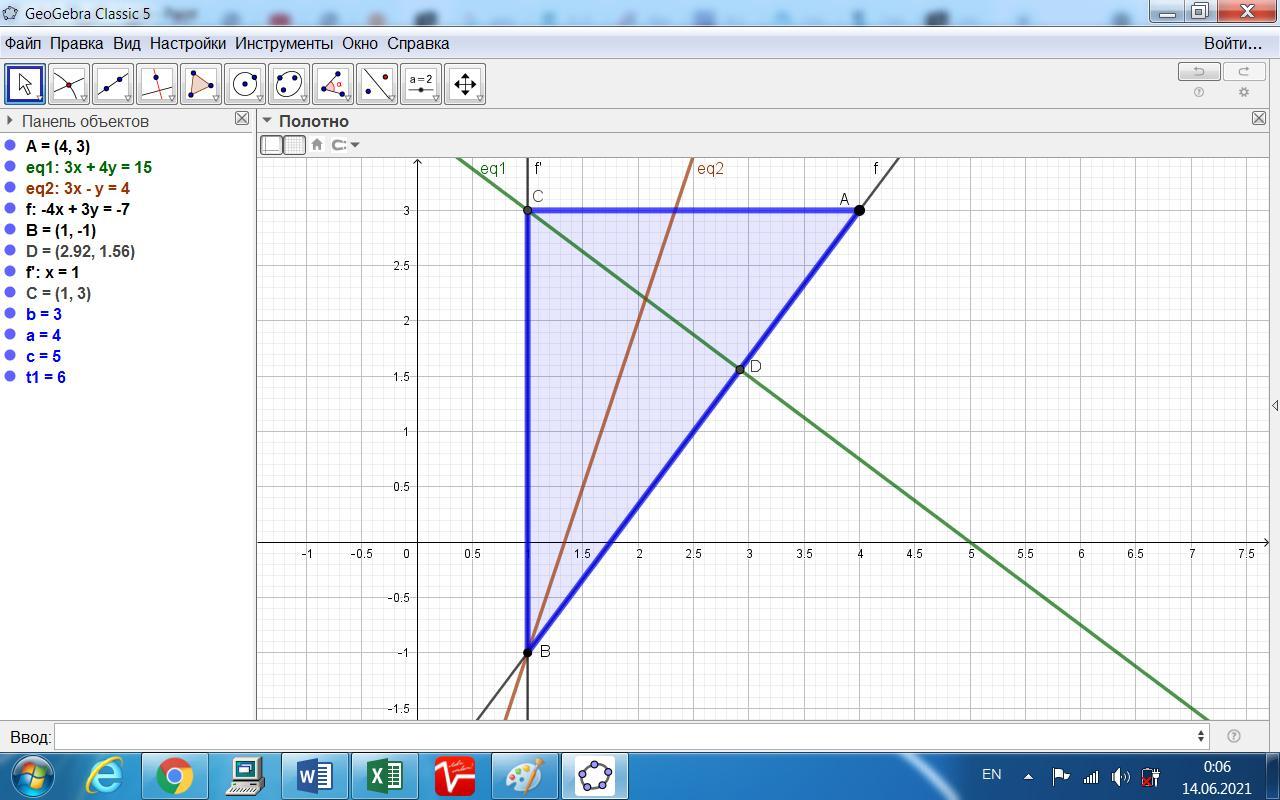
Скласти рівняння сторін трикутника ABC , якщо відомо рівняння висоти CD: 3x + 4y − 15=0, бісектриси BL: 3x − y − 4 = 0 і координати вершини A (4; 3)
Ответы
Даны уравнения высоты CD: 3x + 4y − 15=0, биссектрисы BL: 3x − y − 4 = 0 и координаты вершины A (4; 3) треугольника АВС.
Находим уравнение стороны АВ как перпендикуляра к высоте CD (используя свойство перпендикулярной прямой: коэффициенты А и В меняются на В и (-А)).
AB: 4x - 3y + C = 0, подставляем координаты точки А.
4*4 - 3*3 + С = 0, отсюда С = 9 - 16 = -7.
Уравнение АВ: 4х - 3у - 7 = 0.
Находим координаты точки В как точки пересечения АВ и BL.
4x - 3y - 7 = 0, 4x - 3y - 7 = 0
3x - y - 4 = 0 умн.на-3 = -9x + 3y + 12 = 0
-5x + 5 = 0, x = 5/5 = 1.
y = 3x - 4 = 3*1 - 4 = -1.
Точка В(1; -1).
Переходим к стороне ВС как симметричной АВ относительно BL.
Угловые коэффициенты прямых:
k1(AB) = (4/3), k2(BL) = 3.
Тангенс угла между ними (разность угловых коэффициентов) опредляем по формуле:
k = (k2 - k1) / (1 + k2*k1) = (3 - (4/3)) / (1 + 3*(4/3)) = 1/3.
Находим k(BC) = (3 + (1/3)) / (1 - 3*(1/3)) = ∞.
То есть, ВС - это вертикальная линия с уравнением х = 1.
Уравнение ВС: х = 1.
Определяем координаты точки С при х = 1.
у(С) = (15 - 3*1) / 4 = 3. Точка С(1; 3).
Так как по оси Оу координата совпадает, то это - горизонтальная линия с у = 3.
Уравнение АС: у = 3.