Предмет: Математика,
автор: katiakanavets
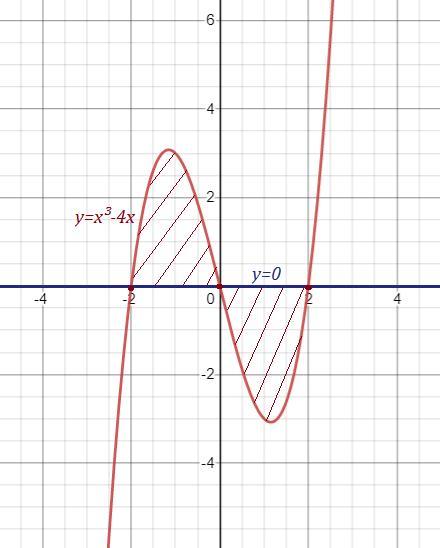
обчисліть площу фігури обмеженої лініями y=x^3-4x y=0
Ответы
Автор ответа:
1
Ответ:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: oksankazakharo
Предмет: Русский язык,
автор: nastena5256
Предмет: Русский язык,
автор: валерия239
Предмет: Химия,
автор: evilgame228
Предмет: Русский язык,
автор: lilitgulip5jni8