Question

Бросают одновременно два игральных кубика, на гранях которых расположены числа от 1 до 6.

*1) Количество способов выпадения четного числа?*
A) 3
B) 9
C) 6
D) 4
E) 2
*2) Количество способов выпадения нечетного числа*
A) 3
B) 2
C) 6
D) 4
E) 9
*3) Сколькими способами может выпасть в сумме число 5?*
A) 3
B) 6
C) 9
D) 4
E) 2
*4) Сколькими способами может выпасть в сумме четное число?*
A) 10
B) 16
C) 18
D) 14
E) 12
*5) Какова вероятность того, что сумма чисел на двух игральных кубиках будет чётным числом.*
A) $\frac{1}{2\\}$
B) $\frac{1}{6}$
C) $\frac{1}{4}$
D) $\frac{1}{9}$
E) $\frac{1}{3}$

Answer 1

Ответ:

↓↓↓

Пошаговое объяснение:

1) Количество способов выпадения четного числа 6

Т.к. на первом кубике 2,4,6  и на втором кубике 2,4,6. Ответ С

2) Количество способов выпадения нечетного числа 6

Т.к. на первом кубике 1,3,5  и на втором кубике1,3,5. Ответ С

3) Четырьмя  способами может выпасть в сумме число 5

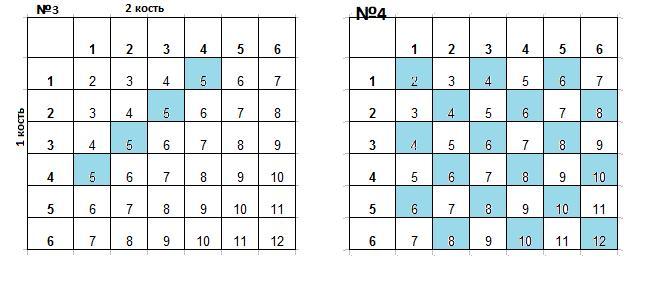
В таблице  в каждую ячейку записана сумма числа очков выпавших на первой и второй кости. Нужные ячейки -синие. Их 4.

Ответ D

4) Восемнадцатью  способами может выпасть в сумме четное число.

В таблице  в каждую ячейку записана сумма числа очков выпавших на первой и второй кости. Нужные ячейки -синие. Их 18.

Ответ С

5) Вероятность того, что сумма чисел на двух игральных кубиках будет чётным числом равна 1/2.

Общее число исходов n=36,  число благоприятствующих исходов  m=18 из п.4. Тогда вероятность события    P=m/ n=18 /36=1/2.

Ответ A