Предмет: Алгебра,
автор: evgeniy8705
Помогите пожалуйста прояснить один момент в примере.
На первом скриншоте дан сам пример.
На втором же предоставлено решение и разъяснение.
Так вот, можете более простым языком прояснить момент с написанием ответа. Что это за условие |x| > |a| и почему именно оно. И как потом считается ответ.
не совсем понятен этот момент.
С самим решением можно сказать разобрался, сложность возникает именно в этих модулях и условиях.
Приложения:
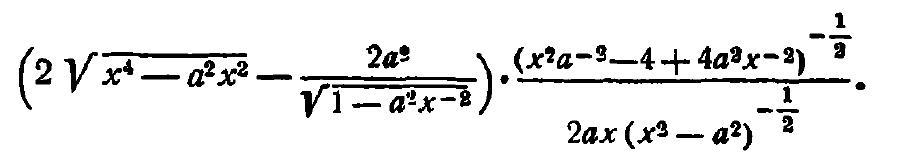

Simba2017:
(x^2)^(1/2)=|x|
Ответы
Автор ответа:
1
бьОтвет:
Дробь в числителе имеет неотрицательное выражение при любом "х" , то есть Тогда, чтобы вся дробь была неотрицательной, надо, чтобы знаменатель был положительным ( нулю равняться он не может), то есть необходимо, чтобы выполнялось неравенство:
Чтобы определить , каким должен быть "х" , надо извлечь квадратный корень из обеих частей неравенства. Известно правило извлечения корней из квадрата какого-либо выражения: .
Поэтому
Похожие вопросы
Предмет: Русский язык,
автор: sabina1112
Предмет: Окружающий мир,
автор: alicenya
Предмет: Русский язык,
автор: VslavaS
Предмет: Математика,
автор: aniutae0122
Предмет: Українська мова,
автор: TheCandyCat