решите неравенство с объяснениями 36^x-1/2-7 * 6^x-1 +1 >=0
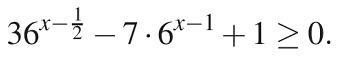
Ответы
Ответ:
хє (-∞;0] U [1;+∞)
Объяснение:
пусть 6^(х-1)=а >0
тогда
36^(х-1/2)=36^(х-1+1/2)=
=36^(х-1)*36^(1/2)=6^2^(х-1)*√36=
=(6^(х-1))^2 * 6
→
36^(x-1/2) - 7*6^(x-1) +1 ≥0 ←→
(6^(х-1))^2 * 6 - 7*6^(x-1) +1 ≥0 ←→
а^2 * 6 - 7 * а + 1 ≥ 0
или 6а² -7а+1≥0
Д = (-7)²-4*6*1=49-24=25=5²>0
а1=(7+5)/(6*2)=12/12=1
а2=(7-5)/(6*2)=2/12=1/6
6а² -7а+1≥0 ←→ 6*(а-1)(а-1/6)≥0
+. -. +
------•-------•------›
1/6. 1. а
а є (-∞;1/6] U [1;+∞)
с учётом одз (а>0) получаем:
а є (0 ;1/6] U [1;+∞)
Выход из замены:
1) а>0 и а≤1/6, а=6^(х-1)
а>0 (при любом х)
а≤1/6 → 6^(х-1)≤1/6
6^(х-1)≤6^(-1)
6>1 → х-1≤-1
х≤0
2) а≥1, а=6^(х-1)
6^(х-1)≥1
6^(х-1)≥6^0
6>1 → х-1≥0
х≥1
Объединяя получаем:
хє (-∞;0] U [1;+∞)
Теория:
Объяснение:
;
;
;
;
Пусть , тогда
;
;
Решением этого неравенства является промежуток t∈(0;1]U[6;+∞)
Вернёмся к замене:
Если , то
(Т.к. по определению любое число в степени строго больше нуля, то мы можем не писать )
Если , то
Ответ: х∈(-∞;0]U[1;+∞)