Предмет: Математика,
автор: fastranner
Исследовать ряд на сходимость:
Приложения:
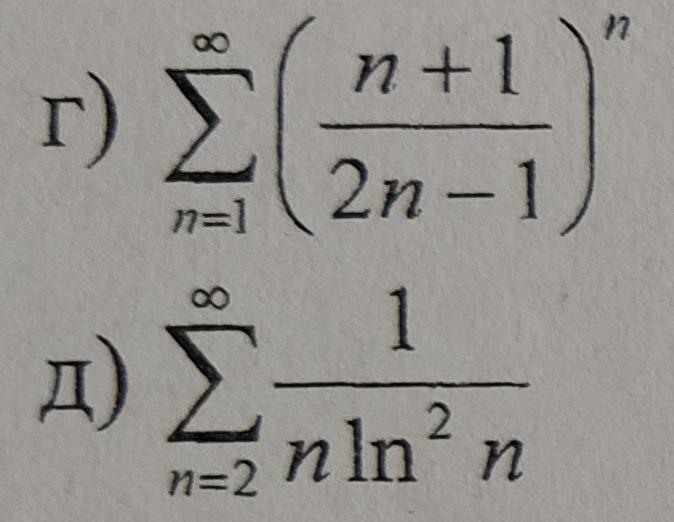
bearcab:
оба сходятся
Ответы
Автор ответа:
1
Ответ:
г) сходится
д) сходится
Пошаговое объяснение:
г)
Используем радикальный признак Коши:
Так как предел меньше 1, то ряд сходится.
д)
- определена и непрерывна на
- монотонно не возрастает:
По интегральному признаку:
Так как интеграл сходится, то ряд сходится.
Спасибо!
Всё бы ничего, но первообразную я взял неправильно.
Автор ответа:
1
Ответ:
Оба ряда сходятся
Пошаговое объяснение:
Решение в приложении
Приложения:


Спасибо!
Похожие вопросы
Предмет: Русский язык,
автор: данил396
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Информатика,
автор: ПОМОГИТЕЕЕЕ1111
Предмет: Русский язык,
автор: ажтащнмдпдпе