Предмет: Геометрия,
автор: markianzavodov
геометрия, помогите пж, 20 баллов
Задача:
Бісетриса кута при оснрві рівнобедреного трикутника дорівнює стороні трикутника. Знайти кути трикутника.
markianzavodov:
Сори, дал 10 баллов, смогу зделать ещё одну такую задачу елементарную на 10
Ответы
Автор ответа:
0
Ответ:
Объяснение:
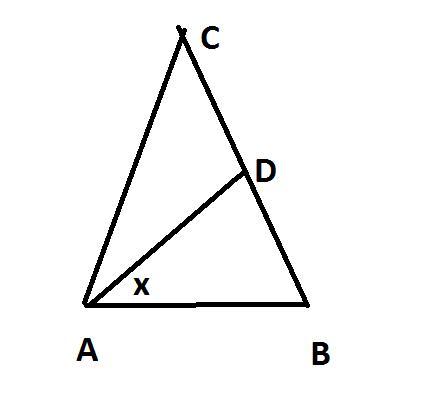
AB=BC; AD=DC
AD-биссектриса
Обозначим ∠BAD=∠DAC=x ; A=2x
углы при основании равнобедренного треугольника равны ⇒
∠C=∠A=2x
∠ADC=180°-x-2x=180°-3x
∠ADC -равнобедренный треугольник ⇒∠ADC=∠C
18°0-3x=2x
180°=5x
x=180°/5=36°
∠A=∠C=2x=2*36=72°
∠B=180-72-72=180-144=36°
Приложения:
Автор ответа:
0
Ответ:
36°, 72°, 72°
Объяснение:
Дано:
АВ=ВС
АК - биссектриса
АК = АС
---------------------------------
∠А, ∠В, ∠С - ?
∠А = 2∠α, т.к. АК - биссектриса ∠А
∠А = ∠С = 2α, т.к. ΔАВС - равнобедренный и, значит, углы при основании равны.
∠АКС = ∠С = 2α, т.к. ΔАКС - равнобедренный (АК=АС) и углы при основании равны.
Сумма углов Δ-ка = 180°, следовательно,
α + 2α +2α = 180°
5α = 180°
α = 180° / 5
α = 36°
∠А = ∠С = 2α = 2 * 36° = 72°
∠В = 180° - 72°*2 =36°
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: lera2986
Предмет: Технология,
автор: KumaChan12
Предмет: Русский язык,
автор: imaevartur2015
Предмет: Математика,
автор: misavoznia
Предмет: Русский язык,
автор: Sasha20101405