Question

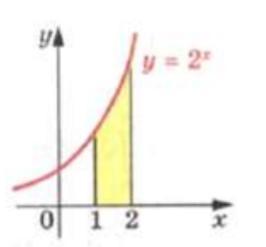
Знайдіть площу криволінійної трапеції, зображеної на рисунку
(с решением)

Answer 1

Ответ:

площадь криволинейной трапеции равна        $\displaystyle \boldsymbol {S=\frac{2}{ln(2)}}$

Объяснение:

Площадь криволинейной трапеции считается по формуде Ньютона-Лейбница

$\displaystyle \int\limits^a_b {\bigg (y_1(x)-y_2(x)\bigg )} \, dx$

В нашем случае

а = 2

b = 1

y₁(x) = $\displaystyle 2^x$

y₂(x) = 0

Теперь считаем интеграл

$\displaystyle S=\int\limits^2_1 {(2^x)} \, dx = \frac{2^x}{ln(2)} \bigg |_1^2=\frac{2^2}{ln(2)} -\frac{2^1}{ln(2) } =\frac{2}{ln(2)}$

Таким образом, мы вычислили площадь криволинейной трапеции.

#SPJ3