Предмет: Математика,
автор: ffnfjtjtkkrk
Острый угол ромба равен 30 °. Радиус круга, вписанного в ромб, равен 3. Найдите площадь ромба.
Ответы
Автор ответа:
0
Ответ:
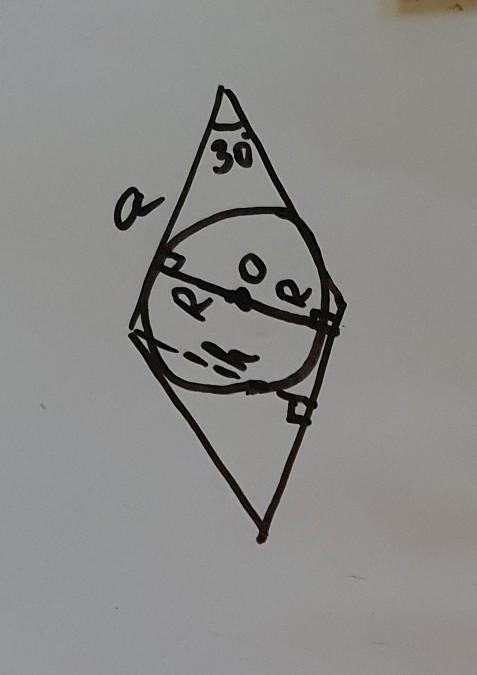
рисунок чисто схематический для наглядности
- стороны ромба образующие острый угол являются касательными проведенными из одной точки к окружности => радиус окружности перпендикулярен стороне в точке касания. =>
- диаметр окружности совпадает с высотой ромба
- h = d = 2r = 2×3 = 6
- через формулу, зная синус острого угла и высоту, найдем сторону ромба
5. найдем площадь ромба через сторону и высоту.
S = ah = 12 × 6 = 72
Приложения:
Автор ответа:
0
Ответ: 72.
Пошаговое объяснение:
Высота ромба 6 ; Сторона ромба 12 (лежит против угла в 30°).
Sр=12*6=72.
Похожие вопросы
Предмет: Английский язык,
автор: metleb1205
Предмет: Английский язык,
автор: familiaavram29
Предмет: Русский язык,
автор: qwert91
Предмет: Обществознание,
автор: MixIxed
Предмет: Русский язык,
автор: ангелинаорловайте