ДАЮ 30 БАЛЛОВ ПОМОГИТЕ РЕШИТЬ ОБЪЯСНИТЕ Срочно,помогите пожалуйста
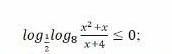
Ответы
Ответ:
x ∈ ( -4; 3.5-√(177/4)] ∪ [3.5+√(177/4); +∞)
Пошаговое объяснение:
log₀₅ log₈[(x²+x)/(x+4)] ≤0;
рассмотрим вначале выражение log₀₅ (f(x)) ≤0, (где f(x)= log₈[(x²+x)/(x+4)])
функция логарифма с основанием 1/2 - убывающая на всей области определения. Т.е. log₀₅ (f(x))=0 при значении f(x)=1, и log₀₅ (f(x))>0 при значении f(x)<1. Следовательно можно записать:
f(x)≥0; log₈[(x²+x)/(x+4)]≥1;
а вот функция log₈[(x²+x)/(x+4)] возрастающая на всей своей области определения т.к. основание логарифма больше 1, поэтому:
(x²+x)/(x+4)]≥8¹;
(x²+x)/(x+4)]≥8;
Перед решением неравенства найдем интервалы допустимых значений переменной х.
1. Оба множителя положительные:
x+4≠0; x≠ -4;
x+4>0; x>-4; x∈ (-4; +∞);
x²+x>0; x(x+1)>0; x>0; x>-1; x ∈ (-∞; -1)∪(0; +∞)
x∈(-4; +∞) ∩ x∈ (-∞; -1)∪(0; +∞);
x∈ (-4; -1)∪(0; +∞)
2. Оба множителя отрицательные:
x+4≠0; x≠ -4;
x+4<0; x<-4; x∈ (-∞; -4);
x²+x<0; x(x+1)<0; x∈( -1;0)
x∈ (-∞; -4) ∩ x∈( -1;0)
x∈∅.
интервалы допустимых значений переменной х: (-4; -1)∪(0; +∞).
Теперь решаем квадратичное неравенство:
(x²+x)/(x+4)]≥8;
(x²+x)/(x+4)-8≥0; (x²+x-8x-32)/(x+4)≥0; (x²-7x-32)/(x+4)≥0; √D=√(49+4*32)=√177;
x₁₂=0.5(7±√177); x₁=3.5+√(177/4); x₂=3.5-√(177/4);
x∈(-∞; 3.5-√(177/4)] ∪ [3.5+√(177/4); +∞);
Сравним этот промежуток с областью определения функции. Учтем, что √(177/4)≈6,7, следовательно 3,5-6,7≈ -3,15.
x∈(-∞; 3.5-√(177/4)] ∪ [3.5+√(177/4); +∞) ∩ x∈ (-4; -1)∪(0; +∞)
x ∈ ( -4; 3.5-√(177/4)] ∪ [3.5+√(177/4); +∞)