Question

Решите задачу:
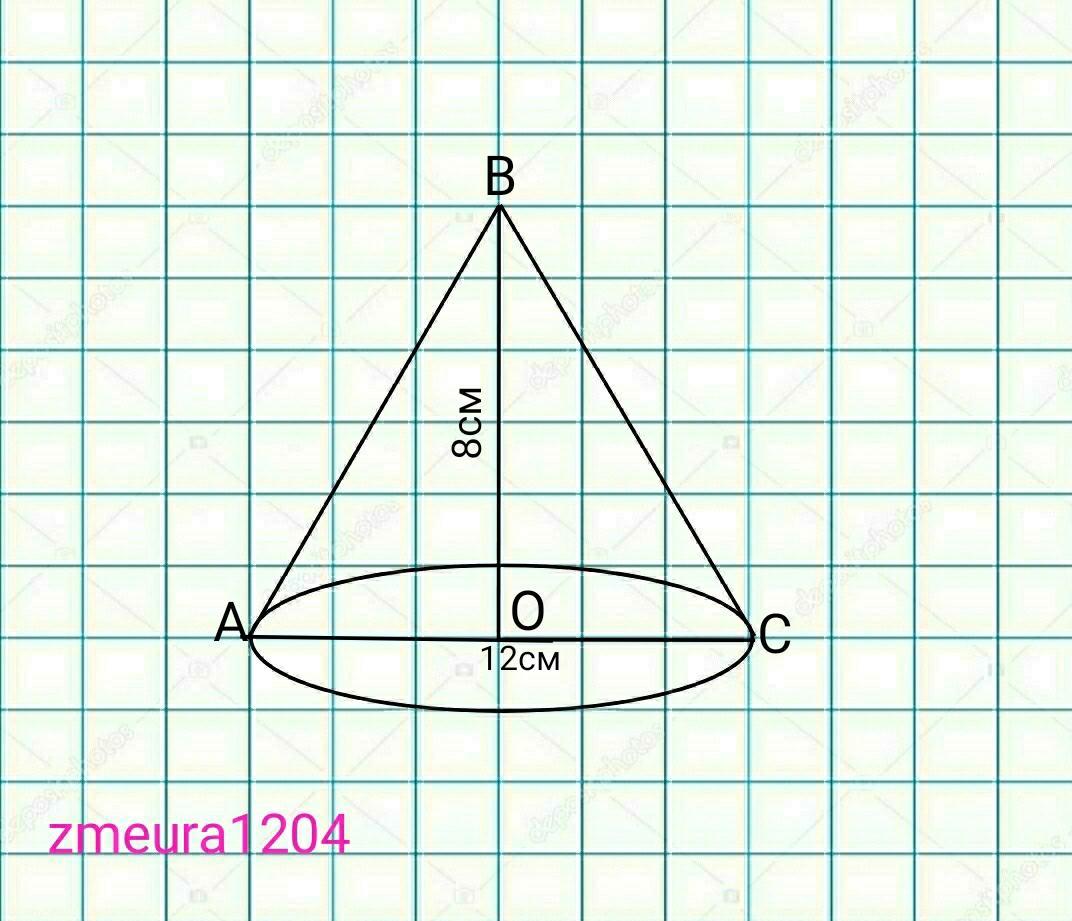
Найдите площадь полной поверхностии и объем конуса, если высота равна 8 см, а диаметр основания 12см.​

Answer 1

Ответ:

Sпол=96π см²

V=96π см³

Пошаговое объяснение:

АО- радиус.

АО=АС/2=12/2=6см. радиус

∆ВОА- прямоугольный треугольник.

По теореме Пифагора

АВ=√(ВО²+АО²)=√(6²+8²)=√(36+64)=

=√100=10см.

Sбок=πRL=π*АО*АВ=π*6*10=60π см²

Sосн=πR²=π*AO²=6²π=36π см²

Sпол=Sбок+Sосн=60π+36π=96π см²

V=1/3*Sосн*ВО=1/3*36π*8=96π см³

Answer 2

Пошаговое объяснение:

h=8 cм

d=12 cм

Найти : S V

S=пи×r×(r+L)

L образующая

r=d/2=12/2=6 cм

По теореме Пифагора :

L=корень(d^2+h^2)=корень (6^2+8^2)=

=корень (36+64)=10 см

S=3,14×6×(6+10)=3,14×96=301,44 cм^2

V=(пи×r^2×h) /3

V=3,14×6^2×8 /3=3,14×36×8 /3=301,44 cм^3