Предмет: Алгебра,
автор: Nurzhan94
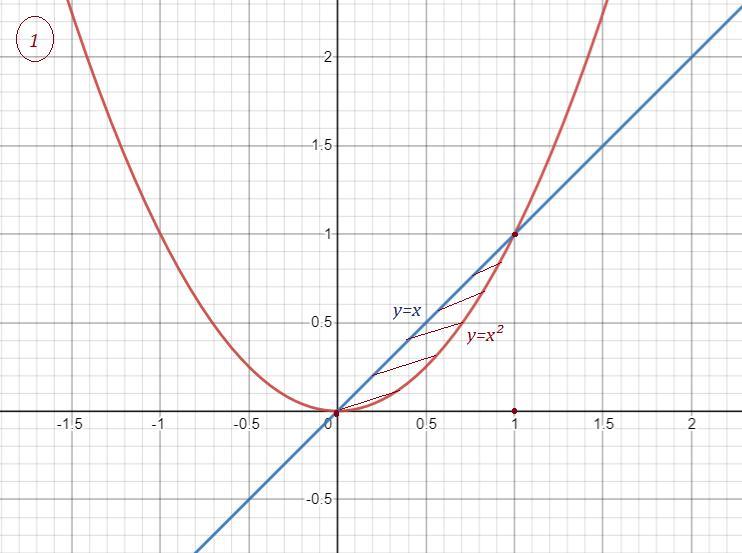
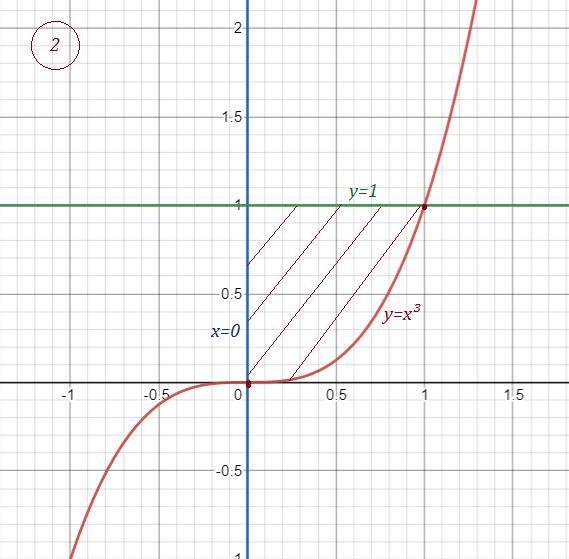
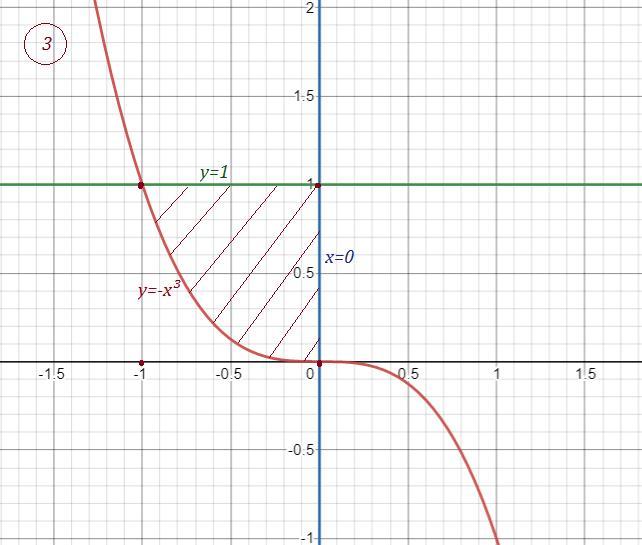
найдите площадь плоской фигуры ограниченной линиями
Приложения:

Ответы
Автор ответа:
2
Ответ:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: sashamlk
Предмет: Другие предметы,
автор: kroshca09
Предмет: Другие предметы,
автор: zima8
Предмет: Окружающий мир,
автор: NikoMills