Предмет: Математика,
автор: INIGO
ПРОШУ ПОМОЩИ!
Решите пожалуйста однородное тригонометрическое уравнение.
Буду очень благодарен.
Даю 20 баллов
Приложения:
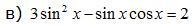
Ответы
Автор ответа:
1
3 sin^2 x - sin x cos x = 2
3 sin^2 x - sin x cos x = 2 (sin^2 x + cos^2 x)
sin^2 x - sin x cos x - 2 cos^2 x = 0
Уравнение однородное 2 степени. Разделим его на cos^2 x
tg^2 x - tg x - 2 = 0
tg x = y
y^2 - y - 2 = 0
D = 9 > 0
y = (1 + 3) / 2 = 2 или y = (1 - 3) / 2= -1
tg x = 2 => x = arctg 2 + πn,n∈Z
tg x = -1 => x = - π / 4 + πk,k∈Z
Автор ответа:
2
Перед нами однородное уравнение. Докажем, что (По ОТТ) не подходят:
1 ≠ 0
Значит мы свободно можем поделить обе части уравнения на :
; n ∈ Z
; n ∈ Z
Похожие вопросы
Предмет: Русский язык,
автор: АльБИНа200гусейнова
Предмет: Английский язык,
автор: stepanyan00
Предмет: Немецкий язык,
автор: weronika4
Предмет: Алгебра,
автор: АртёмДолженЗнать