Предмет: Математика,
автор: sobakazabiyaka
Найти массу кривой L, если плотность кривой в каждой ее точке равна ординате этой точки
Приложения:
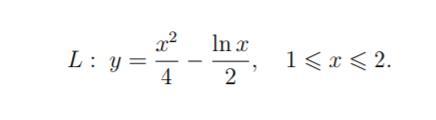
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Так как вид уравнения кривой явный, масса вычисляется по формуле
igorShap:
Прошу прощения, в первом интеграле я неверно записал, корень из 1+(y')^2 не нужен, он входит в дифференциал dl [на дальнейшие расчеты это не влияет]
Похожие вопросы
Предмет: Английский язык,
автор: Елена131313
Предмет: Русский язык,
автор: lubovnovik2015
Предмет: Русский язык,
автор: тимур193
Предмет: Математика,
автор: egorbokhan