Предмет: Геометрия,
автор: riko20520
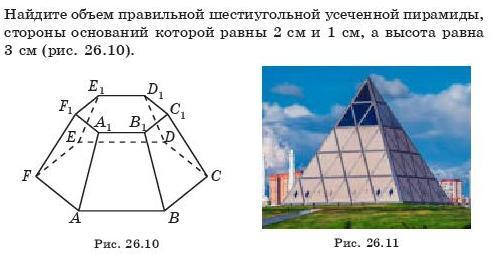
Найдите объем правильной шестиугольной усеченной пирамиды, стороны оснований которой равны 2 см и 1 см, а высота равна 3 см (рис. 26.10).
Приложения:
Ответы
Автор ответа:
2
Ответ:
10,5√3 см³
Объяснение:
S1=6*A1B1²√3/4=6*1²√3/4=1,5√3 см² площадь верхнего основания (S(A1B1...F1))
S2=6*AB²√3/4=6*2²√3/4=6√3 cм² площадь нижнего основания (S(AB...F))
V=⅓h(S1+√(S1*S2)+S2)=
=⅓*3(1,5√3+6√3+√(1,5√3*6√3))=
=7,5√3+√27=7,5√3+3√3=10,5√3 см³
Похожие вопросы
Предмет: Русский язык,
автор: kbyf536
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: Jeka01
Предмет: Литература,
автор: SofiaSmile11