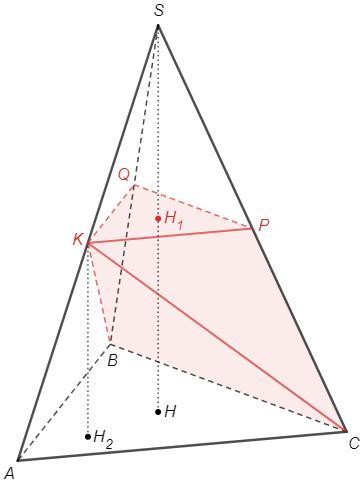
Дана правильная треугольная пирамида SABC, AB = 18, высота SH = 22, точка K - середина AS, точка N - середина BC. Плоскость, проходящая через точку K и параллельная основанию пирамиды пересекает рёбра SB и SC в точках Q и P соответственно. Найдите объем пирамиды KBPQC
Ответы
Ответ:
От исходного объема отсекаем 1/2 и 1/8
V(KBQPC) =3/8 V(SABC) =3/8 *1/3 *√3/4 *18^2 *22 =891√3/4
Объяснение:
Правильная треугольная пирамида, в основании равносторонний треугольник.
S(ABC) =√3/4 AB^2 =81√3
V(SABC) =1/3 S(ABC) SH =1/3 *81√3 *22 =594√3
Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.
KQ||AB, QP||BC, KP||AC
△KSP~△ASC (стороны параллельны), KP/AC =KS/AS =1/2
△KQP~△ABC (стороны параллельны), S(KQP)/S(ABC) =(KP/AC)^2 =1/4
△ASH, KH1||AH, т Фалеса: SH1/SH =KS/AS =1/2
V(SKQP) =1/3 S(KQP) SH1 =1/3 *1/4 S(ABC) *1/2 SH =1/8 V(SABC)
Отрезки параллельных прямых между двумя параллельными плоскостями равны.
KH2 =H1H =1/2 SH
V(KABC) =1/3 S(ABC) KH2 =1/3 S(ABC) 1/2 SH =1/2 V(SABC)
V(KBQPC) =V(SABC) -V(KABC) -V(SKQP) =(1 -1/2 -1/8) V(SABC) =3/8 V(SABC) =891√3/4