Предмет: Математика,
автор: annapetrichenk
Срочно!!! Помогите решить дифференциальное уравнение!
Приложения:
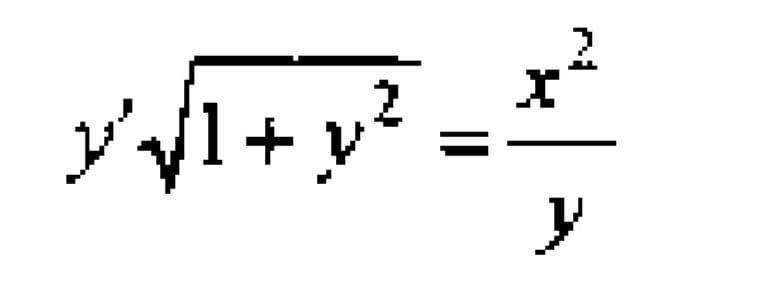
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: lbuzina
Предмет: Қазақ тiлi,
автор: gelia1
Предмет: Английский язык,
автор: paschnyovalex
Предмет: Русский язык,
автор: ВиКтОрИя7185