Предмет: Математика,
автор: ilyacamshh
Пожалуйста помогите
Приложения:
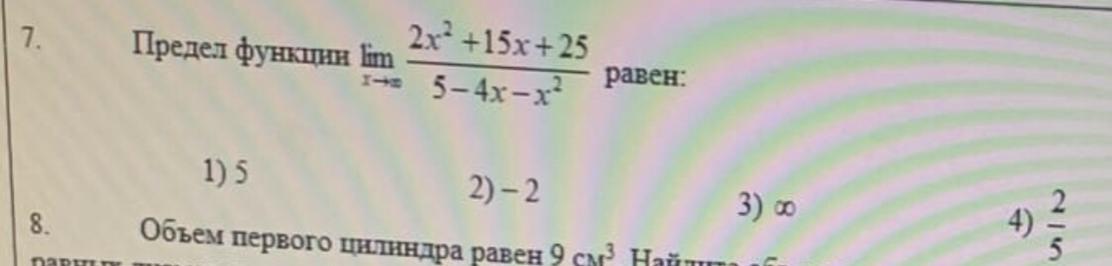
Ответы
Автор ответа:
5
Ответ:
2) -2
Пошаговое объяснение:
Сначала нашли пределы числителя и знаменателя, и, если они: +∞/-∞ - смело можем вынести за скобку общий множитель: x^2 и сократить его. Потом подставляем 0 вместо х, так как лимит стремиться к бесконечности, и получаем ответ.
ilyacamshh:
спасибо!
Похожие вопросы
Предмет: Русский язык,
автор: danyrudik630
Предмет: Немецкий язык,
автор: КатяLUZ
Предмет: Русский язык,
автор: Diana201611
Предмет: Математика,
автор: Дашенька2009