Предмет: Алгебра,
автор: justleyn
cos2x+cos^2x=5/4
Помогите очень нужно
Приложения:
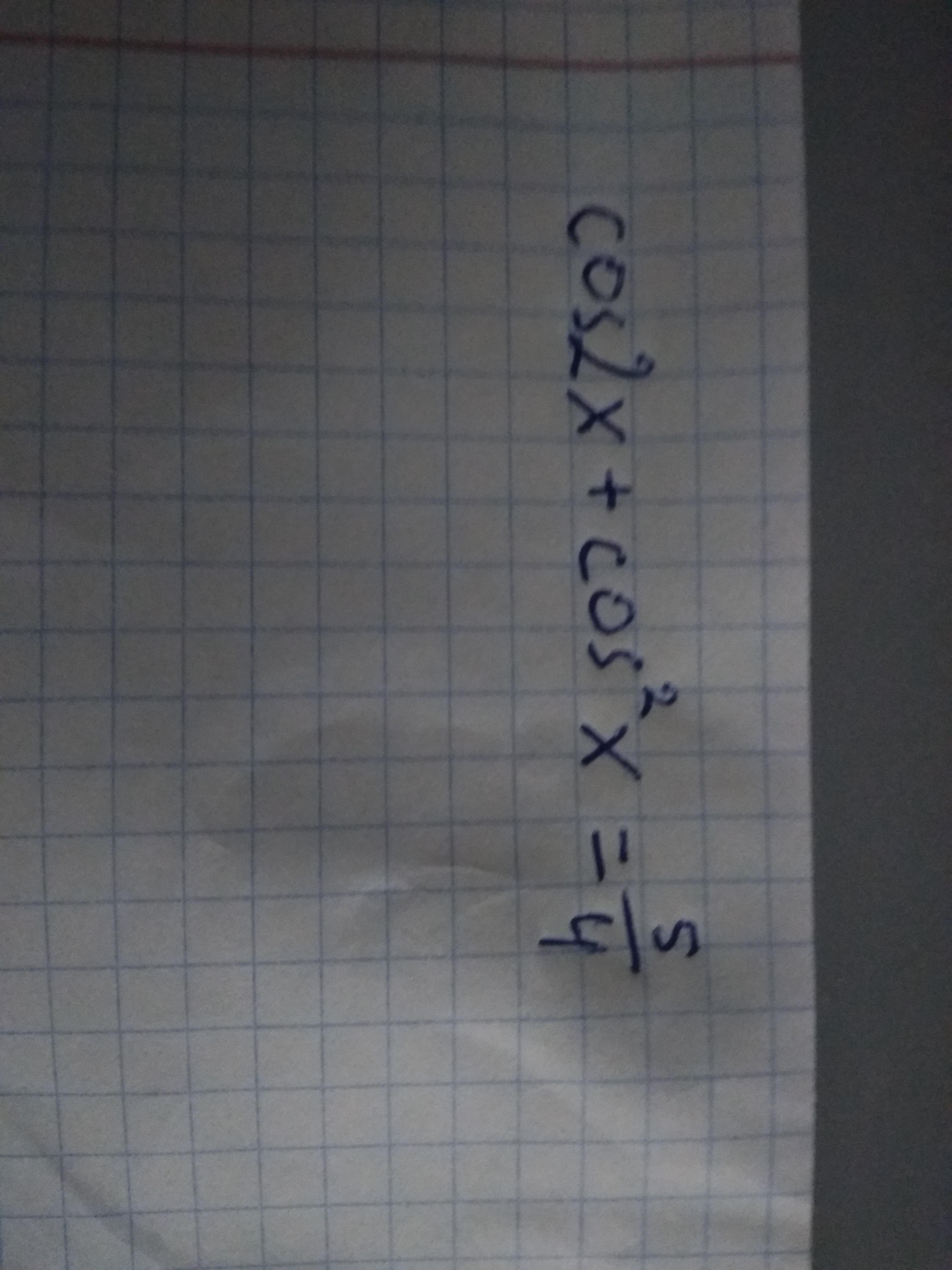
Ответы
Автор ответа:
3
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Окружающий мир,
автор: Germiona15632
Предмет: Русский язык,
автор: enkikigfhd
Предмет: Русский язык,
автор: e200605
Предмет: Литература,
автор: дин87