Предмет: Математика,
автор: koobk83
Преобразуйте выражение: tgx ctg x — cos®а;
3. Преобразуйте выражение: ctg'B(cos®р – 1) + 1
Помогите решить ....
Приложения:
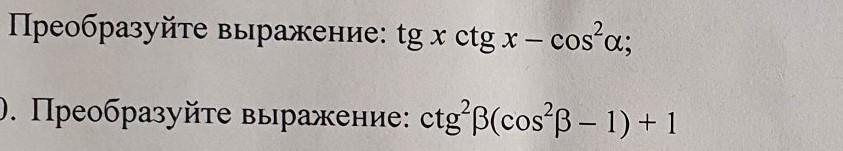
Ответы
Автор ответа:
1
Ответ: 1) sin^2(a), 2) sin^2(b)
Пошаговое объяснение:
1) tg(x) и ctg(x) взаимно обратные функции, ибо tg(x) = sin(x)/cos(x), а ctg(x) = cos(x)/sin(x). Значит их произведение равно единице, т.е. tg(x)*ctg(x) = 1. Итого получаем 1-cos^2(a). Из основного тригонометрического тождества (sin^2(a)+cos^2(a) = 1) приводим полученное 1-cos^2(a) => sin^2(a) + cos^2(a) - cos^2(a) = sin^2(a)
2) Рассмотрим выражение в скобке. cos^2(b)-1=cos^2(b)-sin^2(b)-cos^2(b)=-sin^2(b). Далее умножаем на ctg^2(b). Получаем cos^2(b)*(-sin^2(b))/sin^2(b)=-cos^2(b). Далее -cos^2(b)+1=sin^2(b)
Похожие вопросы
Предмет: Русский язык,
автор: пурга1
Предмет: Русский язык,
автор: clashofclans3289
Предмет: Английский язык,
автор: МэйблПайнс234
Предмет: Обществознание,
автор: bettamatthew
Предмет: Литература,
автор: OlesyaSmotrina